Topper's Solved these Questions
TRIANGLES
OSWAL PUBLICATION|Exercise BOARD CORNER (LONG SHORT ANSWER TYPE QUESTION ( 4 MARK EACH )) |4 VideosTRIANGLES
OSWAL PUBLICATION|Exercise Multiple Choice Questions |14 VideosTRIANGLES
OSWAL PUBLICATION|Exercise BOARD CORNER ( VERY SHORT ANSWER TYPE QUESTION ( 1 MARK EACH )) |4 VideosSURFACE AREAS AND VOLUMES
OSWAL PUBLICATION|Exercise BOARD CORNER (LONG ANSWER TYPE QUESTIONS)|9 Videos
Similar Questions
Explore conceptually related problems
OSWAL PUBLICATION-TRIANGLES-BOARD CORNER ( SHORT ANSWER TYPE QUESTION ( 3 MARK EACH ))
- In the given figure, angle ACB=90^(@) and CD bot AB. Prove that CD^(2...
Text Solution
|
- P and Q are points on the sides C A and C B respectively of A B...
Text Solution
|
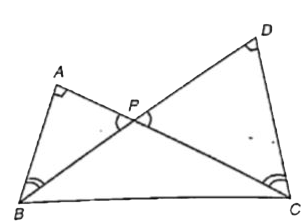
- Two right triangles ABC and DBC are drawn on the same hypotenues BC on...
Text Solution
|
- Diagonals of a trapezium PQRS intersect each other at the point 0 ,PQa...
Text Solution
|
- Prove that the area of an equilateral triangle described on one sid...
Text Solution
|
- If the areas of two similar triangles are equal, prove that they ar...
Text Solution
|