Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NTA MOCK TESTS-NTA TPC JEE MAIN TEST 98-Physics (SUBJECTIVE NUMERICAL)
- Separation energy of a hydrogen like ion from its third excited state ...
Text Solution
|
- Two unknown resistances are connected in two gaps of a meter-bridge. T...
Text Solution
|
- The plates of a parallel plate capacitor are charged to a potential di...
Text Solution
|
- Two seconds after projection, a projectile is travelling in a directio...
Text Solution
|
- The coefficient of friction between the two blocks shown in the figure...
Text Solution
|
- In a resonance tube experiment to determine the speed of sound in air,...
Text Solution
|
- A vessel whose bottom has round holes with diameter of 1 mm is filled...
Text Solution
|
- A point source S is placed at the bottom of a 12 mm high transparent b...
Text Solution
|
- In Young's double slit experiment, how many maxima can be obtained on ...
Text Solution
|
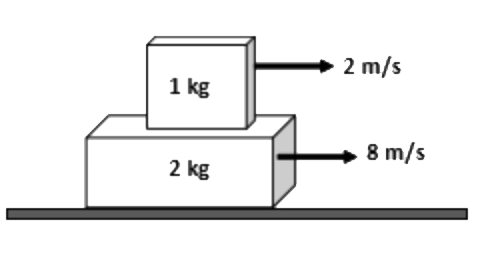
- A block of mass m=1kg moving on a horizontal surface with speed v(i)=2...
Text Solution
|