लिखित उत्तर
Verified by Experts
Recommended Questions
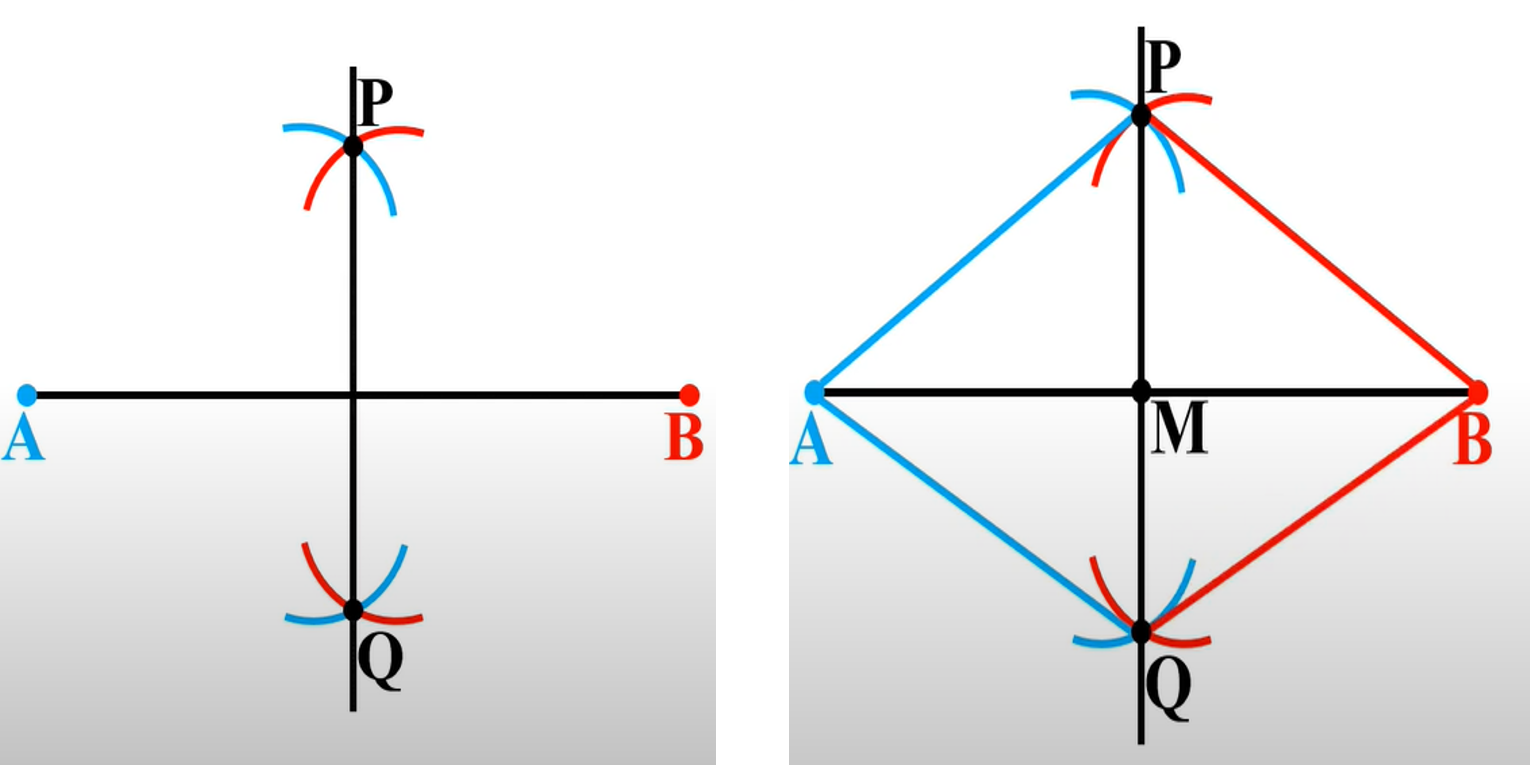
- <b>एक दिए गए रेखाखंड के लंब समद्विभाजक (लंबार्धक) की रचना करना।</b>
Text Solution
|
- निम्नलिखित वाक्यों के रचना के अनुसार भेद पहचानकर लिखिए : ममता कि एक ...
Text Solution
|
- निम्नलिखित वाक्यों की रचना के अनुसार भेद पहचानकर लिखिए : आश्र...
Text Solution
|
- एक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेख...
Text Solution
|
- प्रायोगिक ज्यामिति से जान पहचान |रेखा की रचना करना सीखे
Text Solution
|
- रेखा की रचना |अभ्यास के लिए प्रश्न
Text Solution
|
- दिए गए व्यापक हल वाले अवकल समीकरण का निर्माण|दिए गए वक्रों के कुल को न...
Text Solution
|
- दो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु ...
Text Solution
|
- कुछ विशेष कोणों की रचना|दी गयी रेखा के लम्ब समद्विभाजक की रचना
Text Solution
|