एक त्रिभुज `ABC` में आधार `BC`, एक आधार कोण माना `angle B` तथा दो अन्य भुजाओं का अंतर `(AB-AC)` या `(AC-AB)` दिया है।
हमको त्रिभुज `ABC` की रचना करनी है।
यहाँ निम्न दो ही स्थितियाँ हो सकती हैं :
स्थिति (i) : माना कि `AB gt AC` अर्थात `AB-AC` दिया है।
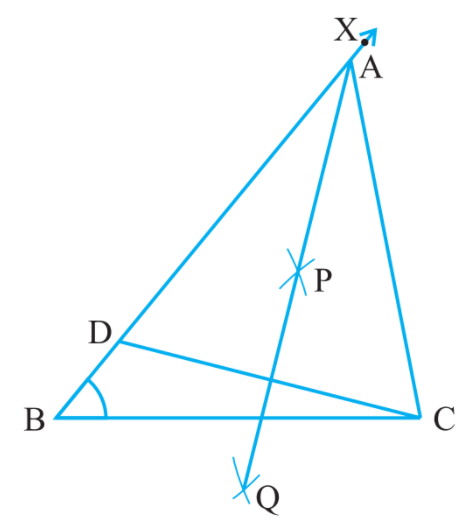रचना के चरण : चरण 1 : आधार `BC` खींचिए और बिन्दु `B` पर दिए गए कोण के बराबर एक कोण, मान लीजिए कोण `XBC` बनाइए।
चरण 2 : किरण `BX` से `AB - AC` के बराबर रेखाखंड `BD` काटिए।
चरण 3 : `DC` को मिलाइए और `DC` का लंब समद्विभाजक `PQ` खींचिए।
`PQbotDC`
चरण 4 : माना कि `PQ` किरण `BX` को बिन्दु `A` पर प्रतिच्छेद करता है। `AC` को मिलाइए (देखिए आकृति)
अतः `ABC` अभीष्ट त्रिभुज है।
व्याख्या : आइए अब देखते हैं की किस प्रकार हमने अभीष्ट त्रिभुज प्राप्त किया है।
दिए गए मापन के अनुसार आधार `BC` और `angleB` बनाए गए हैं। बिन्दु `A`, `DC` के लंब समद्विभाजक पर स्थित है।
अतः, `AD = AC`
इसलिए, `BD = AB - AD = AB - AC`
स्थिति (ii) : मान लीजिए `AB lt AC` है, अर्थात् `AC - AB` दिया हुआ है।
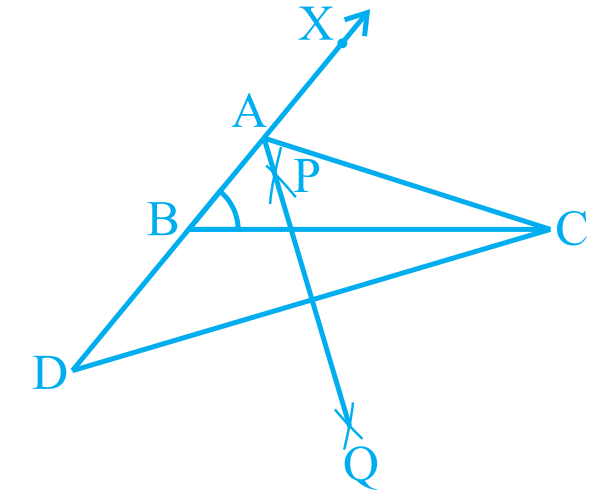रचना के चरण : चरण 1 : आधार `BC` खींचिए और बिन्दु `B` पर दिए गए कोण के बराबर एक कोण, मान लीजिए कोण `XBC` बनाइए।
चरण 2 : विपरीत दिशा में बढ़ी हुई रेखा `BX` से `AC – AB` के बराबर एक रेखाखंड `BD` काटिए।
चरण 3 : `DC` को मिलाइए तथा `DC` का लंब समद्विभाजक `PQ` खींचिए।
चरण 4 : मान लीजिए कि `PQ`, `BX` को `A` पर प्रतिच्छेद करती है।
`AC` को मिलाइए (देखिए आकृति)
अतः `ABC` अभीष्ट त्रिभुज है।
व्याख्या : आइए अब देखते हैं की किस प्रकार हमने अभीष्ट त्रिभुज प्राप्त किया है।
दिए गए मापन के अनुसार आधार `BC` और `angleB` बनाए गए हैं। बिन्दु `A`, `DC` के लंब समद्विभाजक पर स्थित है।
अतः, `AD = AC`
इसलिए, `BD = AD - AB = AC - AB`
