Home
Class 12
CHEMISTRY
Several factors (steric, electronic, orb...

Several factors (steric, electronic, orbital interactions etc.) can affect the inversion barrier of an amine. In the given pair which data is correctly placed ?

A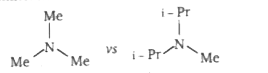


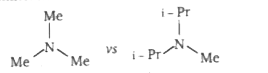
`DeltaG^(pm)=7.9"kcal/mol"DeltaG^(pm)=0.2"kcal/mol"`

B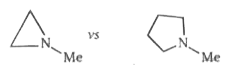


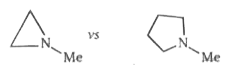
`DeltaG^(pm)=20.5"kcal/mol"DeltaG^(pm)=7.0"kcal/mol"`

C

BOTH A AND B

D

NONE

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • GENERAL ORGANIC CHEMISTRY

    MS CHOUHAN|Exercise LEVEL - 2|95 Videos

  • GENERAL ORGANIC CHEMISTRY

    MS CHOUHAN|Exercise LEVEL - 2 (SUBJECTIVE PROBLEMS )|13 Videos

  • CARBOXYLIC ACID AND THEIR DERIVATIVES

    MS CHOUHAN|Exercise LEVEL-2( SUBJECTIVE PROBLEMS)|1 Videos

  • GRIGNARD REAGENT

    MS CHOUHAN|Exercise Level-2 (Subjective Problems)|6 Videos

Similar Questions

Explore conceptually related problems

The amount of energy released when an electron is added to an isolated gaseous atom to produce a monovalent anion is called electron affinity or first electron affinity or electron gain enthalpy. The first electron is given a negative sign as the addition of an electron to a neutral atom is an exoergic process. The addition of electron to A^(-1) requires energy to overcome the force of repulsion. Thus, the second electron affinity is an endoergic process. The magnitude of electron affinity depends on a number of factors such as (i) atomic size (ii) effective nuclear charge (iii) screening effect (iv) half and fully filled orbitals and (v) shape of orbital. In general, electron affinity increases as the atomic radii decrease in a period. However, there are exceptions when the atoms have stable configurations. In a group, electron affinity decreases as the size increases. However, the members of 3rd period have somewhat higher values than the members in the 2nd period of the same subgroups. Which of the following processes is endoergic in nature ?

The amount of energy released when an electron is added to an isolated gaseous atom to produce a monovalent anion is called electron affinity or first electron affinity or electron gain enthalpy. The first electron is given a negative sign as the addition of an electron to a neutral atom is an exoergic process. The addition of electron to A^(-1) requires energy to overcome the force of repulsion. Thus, the second electron affinity is an endoergic process. The magnitude of electron affinity depends on a number of factors such as (i) atomic size (ii) effective nuclear charge (iii) screening effect (iv) half and fully filled orbitals and (v) shape of orbital. In general, electron affinity increases as the atomic radii decrease in a period. However, there are exceptions when the atoms have stable configurations. In a group, electron affinity decreases as the size increases. However, the members of 3rd period have somewhat higher values than the members in the 2nd period of the same subgroups. Which one of the following arrangements represents the correct order of electron gain enthalpy (with negative sign) of the given atomic species ?

An orbital is designated by certain values of first three quantum numbers (n, l and m) and according to Pauli.s exclusion principle, no two electrons in a atom can have all the for quantum numbers equal. N, l and m denote size, shape and orientation of the orbital. The permissible values of n are 1,2,3.... prop while that of 1 are all possible integral values from 0 to n-n. Orbitals with same values of n and 1 but different values of m (where m can have any integral values from 1 to +1 including zero) are of equal energy and are called degenerate orbitals. However degeneracy is destroyed in homogeneous external magnetic field due to different extent of interaction between the applied field and internal electronic magnet of different orbitals differing in orientations. In octahedral magnetic field external magnetic field as oriented along axes while in tetrahedral field the applied field actas more in between the axes than that on the axes themselves. For 1=0, 1,2,3,...., the states (called sub-shells) are denoted by the symbol s,p,d,f.....respectively. After f, the subshells are denoted by letters alphabetically 1 determines orbital angular motion (L) of electron as L = sqrt(l(l+1))(h)/(2pi) ON the other hand, m determines Z-component of orbital angular momentum as L_(Z) = m((h)/(2pi)) Hund.s rule states that in degenerate orbitals electrons do not pair up unless and until each each orbitals has got an electron with parallesl spins Besides orbital motion,an electron also posses spin-motion. Spin may be clockwise and anticloskwise. Both these spin motions are called two spins states of electrons characterized by spin Q.N (s) : s = +(1)/(2) and = -(1)/(2) respectively The sum of spin Q.N. of all the electrons is called total spin(s) and 2s+1 is called spin multiplicity of the configuration as a whole. The spin angular momentum of an electron is written as L_(s) = sqrt(s(s+1))(h)/(2pi) The orbital angular momentum of electron (l=1) makes an angles of 45^(@) from Z-axis. The L_(z) of electron will be

The amount of energy released when an electron is added to an isolated gaseous atom to produce a monovalent anion is called electron affinity or first electron affinity or electron gain enthalpy. The first electron is given a negative sign as the addition of an electron to a neutral atom is an exoergic process. The addition of electron to A^(-1) requires energy to overcome the force of repulsion. Thus, the second electron affinity is an endoergic process. The magnitude of electron affinity depends on a number of factors such as (i) atomic size (ii) effective nuclear charge (iii) screening effect (iv) half and fully filled orbitals and (v) shape of orbital. In general, electron affinity increases as the atomic radii decrease in a period. However, there are exceptions when the atoms have stable configurations. In a group, electron affinity decreases as the size increases. However, the members of 3rd period have somewhat higher values than the members in the 2nd period of the same subgroups. Which of the following species has the highest electron affinity?

The mixing or redistribution of energy among the atomic orbitals is known as hybridisation. In hybridisation each electron can be described by its wave function psi . In which of the following species lone pair - bond pair repulsion is maximum

Bond Length: Internuclear distance between two adjacent atoms in an species is known as bond length, -Bond length depends on: i) size of the atom involved in the bond formation ii) size of the orbitals involved in the bond formation iii) Lone pair-long pair repulsion iv) Resonance v) s-character of combining orbitals with the increasing size of the atoms and atomic orbitals bond length increases. Lone pair-lone pair repulsion increases bond length (if atoms are small sized) whereas resonance can increase some bond lengths and decrease some other bond length. With increasing s-character bond length decreases, whereas with increasing multiplicity of bonds, bond length decreases. However, in some cases, bond lengths are also affected by relative position of bonds (between two similar atoms). Usually but not always with increasing bond length, bond strength (and hence bond dissociation energy) decreases. In which of the following all bonds are not equivalent?

The equation of Schroedinger for the hydrogen atom in the time-independet, non-relativistic form is a partial differential equation involving the position coordinates (x, y and z). The potential energy term for the proton-electron system is spherically symmetric of the form -1//4pi in_(0) xx (e^(2)//r) . THus it is advantages to change over from the cartesian coordinates (x,y and z) to the spherical polar coordinates, (r, theta and phi ). In this form the equation become separable in the radial part involving r and the angular part involving theta and phi . The probability of locating the electron within a volume element d tau = 4pi r^(2)dr is then given |Psi|^(2)(4pir^(2)dr) , where Psi is a function of r, theta and phi . With proper conditions imposed on Psi , the treatment yields certain functions, Psi , known as atomic orbitals which are solutions of the equations. Each function Psi correspods to quantum number n, l and m, the principal, the azimuthal and the magnetic quantum number respectively, n has values 1, 2, 3,...., l has values 0, 1, 2, ....(n-1) for each value of n and m (n-1) for each value of n and m (m_(l)) has values =1, +(l+1),...1,0,-1,-2...-l i.e., (2l+1) values for each value of l. In addition a further quantum number called pin had to be introduced with values +-1//2 . Any set of four values for n, l , m and s characterizes a spin orbital. Pauli.s exclusion principle states that a given spin orbital can accomodate not more than electron. Further the values l = 0, l=1, l=2, l=3 are designated s,p,d and f orbitals respectively. It is a basic fact that any two electrons are indistinguishable. 3 electrons are to be accomodated in the spin orbitals included under the designated 2p, conforming to the Pauli principle. Calculate the number of ways in which this may be done.

The equation of Schroedinger for the hydrogen atom in the time-independet, non-relativistic form is a partial differential equation involving the position coordinates (x, y and z). The potential energy term for the proton-electron system is spherically symmetric of the form -1//4pi in_(0) xx (e^(2)//r) . THus it is advantages to change over from the cartesian coordinates (x,y and z) to the spherical polar coordinates, (r, theta and phi ). In this form the equation become separable in the radial part involving r and the angular part involving theta and phi . The probability of locating the electron within a volume element d tau = 4pi r^(2)dr is then given |Psi|^(2)(4pir^(2)dr) , where Psi is a function of r, theta and phi . With proper conditions imposed on Psi , the treatment yields certain functions, Psi , known as atomic orbitals which are solutions of the equations. Each function Psi correspods to quantum number n, l and m, the principal, the azimuthal and the magnetic quantum number respectively, n has values 1, 2, 3,...., l has values 0, 1, 2, ....(n-1) for each value of n and m (n-1) for each value of n and m (m_(l)) has values =1, +(l+1),...1,0,-1,-2...-l i.e., (2l+1) values for each value of l. In addition a further quantum number called pin had to be introduced with values +-1//2 . Any set of four values for n, l , m and s characterizes a spin orbital. Pauli.s exclusion principle states that a given spin orbital can accomodate not more than electron. Further the values l = 0, l=1, l=2, l=3 are designated s,p,d and f orbitals respectively. Which of the following diagrams corresponds to the 2s orbital ?

The equation of Schroedinger for the hydrogen atom in the time-independet, non-relativistic form is a partial differential equation involving the position coordinates (x, y and z). The potential energy term for the proton-electron system is spherically symmetric of the form -1//4pi in_(0) xx (e^(2)//r) . THus it is advantages to change over from the cartesian coordinates (x,y and z) to the spherical polar coordinates, ( r, theta and phi ). In this form the equation become separable in the radial part involving r and the angular part involving theta and phi . The probability of locating the electron within a volume element d tau = 4pi r^(2)dr is then given |Psi|^(2)(4pir^(2)dr) , where Psi is a function of r, theta and phi . With proper conditions imposed on Psi , the treatment yields certain functions, Psi , known as atomic orbitals which are solutions of the equations. Each function Psi correspods to quantum number n, l and m, the principal, the azimuthal and the magnetic quantum number respectively, n has values 1, 2, 3,...., l has values 0, 1, 2, ....(n-1) for each value of n and m (n-1) for each value of n and m (m_(l)) has values =1, +(l+1),...1,0,-1,-2...-l i.e., (2l+1) values for each value of l. In addition a further quantum number called pin had to be introduced with values +-1//2 . Any set of four values for n, l , m and s characterizes a spin orbital. Pauli.s exclusion principle states that a given spin orbital can accomodate not more than electron. Further the values l = 0, l=1, l=2, l=3 are designated s,p,d and f orbitals respectively. How many spin orbitals are there corresponding to n = 3?

An orbital is designated by certain values of first three quantum numbers (n, l and m) and according to Pauli.s exclusion principle, no two electrons in a atom can have all the for quantum numbers equal. N, l and m denote size, shape and orientation of the orbital. The permissible values of n are 1,2,3.... prop while that of 1 are all possible integral values from 0 to n-n. Orbitals with same values of n and 1 but different values of m (where m can have any integral values from 1 to +1 including zero) are of equal energy and are called degenerate orbitals. However degeneracy is destroyed in homogeneous external magnetic field due to different extent of interaction between the applied field and internal electronic magnet of different orbitals differing in orientations. In octahedral magnetic field external magnetic field as oriented along axes while in tetrahedral field the applied field actas more in between the axes than that on the axes themselves. For 1=0, 1,2,3,...., the states (called sub-shells) are denoted by the symbol s,p,d,f.....respectively. After f, the subshells are denoted by letters alphabetically 1 determines orbital angular motion (L) of electron as L = sqrt(l(l+1))(h)/(2pi) ON the other hand, m determines Z-component of orbital angular momentum as L_(Z) = m((h)/(2pi)) Hund.s rule states that in degenerate orbitals electrons do not pair up unless and until each each orbitals has got an electron with parallesl spins Besides orbital motion,an electron also posses spin-motion. Spin may be clockwise and anticloskwise. Both these spin motions are called two spins states of electrons characterized by spin Q.N (s) : s = +(1)/(2) and = -(1)/(2) respectively The sum of spin Q.N. of all the electrons is called total spin(s) and 2s+1 is called spin multiplicity of the configuration as a whole. The spin angular momentum of an electron is written as L_(s) = sqrt(s(s+1))(h)/(2pi) According to Hund.s rule, the distribution of electron within the various orbitals of a given sub-shell is one which is associated with