Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
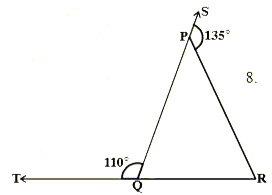
- In the given figure sides QP and RQ of ΔPQR are produced to points S a...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|
- The inequation that best describes the graph given below is <img src=...
Text Solution
|
- The inequation that best describes the following graph is <img src="h...
Text Solution
|
- चित्र में, त्रिभुज PQR की भुजाएँ QP तथा RQ को क्रमशः S तथा T तक बढ़ाया...
Text Solution
|
- चित्र में DeltaPQR की भुजाएँ QP और RQ को क्रमश : बिन्दुओं S और T तक बढ़...
Text Solution
|
- In the attached picture DeltaPQR Arms of QP And RQ Is extended to the ...
Text Solution
|