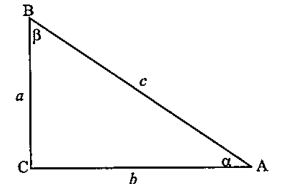
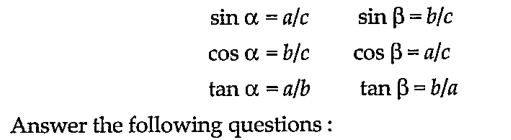A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
OSWAL PUBLICATION-SAMPLE PAPER 4-Section -C
- Case Study-1: Consider a right triangle, where a and b are its length,...
Text Solution
|
- A hemispherical depression is cut out from one face of a cubical block...
Text Solution
|
- Sushant has a vessel in the shape of an inverted cone that is open at ...
Text Solution
|
- Two hoardings are put on two poles of equal heights standing on either...
Text Solution
|
- Two hoardings are put on two poles of equal heights standing on either...
Text Solution
|
- Aadita is celebrating her birthday. She invited her friends. She bough...
Text Solution
|
- Aadita is celebrating her birthday. She invited her friends. She bough...
Text Solution
|
- Aadita is celebrating her birthday. She invited her friends. She bough...
Text Solution
|
- Aadita is celebrating her birthday. She invited her friends. She bough...
Text Solution
|