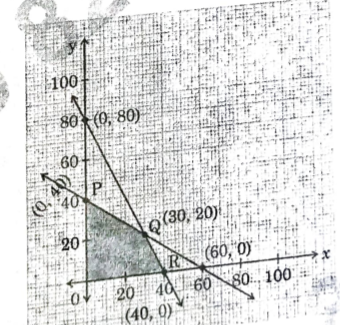
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
XII BOARDS PREVIOUS YEAR-QUESTION PAPER 2022 TERM 1 SET 1-SECTION-C
- In a sphere of radius r, a right circular cone of height h having maxi...
Text Solution
|
- The corner points of the feasible region determined by a set of const...
Text Solution
|
- If curves y^(2) = 4 x and xy = c cut at right angles , then the value ...
Text Solution
|
- The inverse of the matrix X = [{:(2,0,0),(0,3,0),(0,0,4):}]
Text Solution
|
- For an L.P.P. the objective function is Z = 4x + 3y and the feasible ...
Text Solution
|
- In a residential society composing of 100 houses. there were children ...
Text Solution
|
- In a residential society composing of 100 houses. there were children ...
Text Solution
|
- In a residential society composing of 100 houses. there were children ...
Text Solution
|
- In a residential society composing of 100 houses. there were children ...
Text Solution
|
- In a residential society composing of 100 houses. there were children ...
Text Solution
|