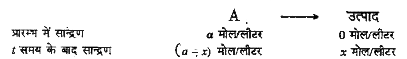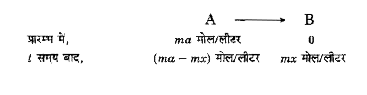अभिक्रिया की कोटि
रासायनिक अभिक्रिया में भाग लेंगे वाले अभिकारकों के उन अणुओं की संख्या जिनका सान्द्रण रासायनिक अभिक्रिया की प्रगति में परिवर्तित होता है, अभिक्रिया की कोटि कहते है।
उदाहरण- एस्टर का जल-अपघटन।
`CH_(3)COOC_(2)H_(5)+H_(2)Ooverset(H^(+))rarrCH_(3)COOH+C_(2)H_(5)OH`
इस अभिक्रिया की प्रगति में अभिकारक के केवल एक अणु (एस्टर) का सान्द्रण परिवर्तित होता है जबकि जल का सान्द्रण अपरिवर्तित रहता है। अतः यह प्रथम कोटि की अभिक्रिया का उदाहरण है।
.प्रथम कोटि की अभिक्रिया. वह अभिक्रिया है, जिसमे अभिकारक के एक अणु का सान्द्रण रासायनिक अभिक्रिया की प्रगति में परिवर्तित होता है अर्थात उसका वेग अभिकारक के सान्द्रण के समानुपाती होता है। उदाहरण के लिए निम्नलिखित अभिक्रिया में केवल शक्कर के एक अणु की सान्द्रता परिवर्तित होती है। अतः यह प्रथम कोटि की अभिक्रिया है।
(1) शक्कर का जल-अपघटन-
`underset("शक्कर")(C_(12)H_(22)O_(11))+H_(2)Ounderset(("तनु HCl या तनु "H_(2)SO_(4)" द्वारा"))overset(H^(+))rarrunderset("ग्लूकोस")(C_(6)H_(12)O_(6))+underset("फ्रक्टोस")(C_(6)H_(12)O_(6))`
(2) एस्टर का जल-अपघटन-
`CH_(3)COOC_(2)H_(5)+H_(2)Ooverset(H^(+))rarrCH_(3)COOH+C_(2)H_(5)OH`
`CH_(3)COOCH_(3)+H_(2)Ooverset(H^(+))rarrCH_(3)COOH+CH_(3)OH`
(3) सभी रेडियोएक्टिव विघटन प्रथम कोटि की अभिक्रिया के उदाहरण है।
गतिक-समीकरण- माना कि कोई प्रथम कोटि कि अभिक्रिया निम्न प्रकार से है-
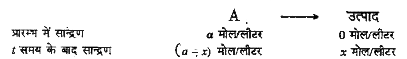
अतः द्रव्य अनुपाती क्रिया के नियमानुसार,
अभिक्रिया का वेग, `(dx)/(dt)prop[A]`
t समय बाद अभिक्रिया का वेग, `(dx)/(dt)=k(a-x)`
या `(dx)/((a-x))=k.dt`
जहाँ k एक स्थिरांक है, जिसे वेग स्थिरांक कहते है।
दोनों पक्षों का समाकलन करने पर,
`int(dx)/(a-x)=intk.dt`
या `-log_(e)(a-x)=kt+I`
जहाँ I = समाकलन स्थिरांक
जब `t=0, x=0` तो `-log_(e)a=I`
I का मान समीकरण (2) में रखने पर,
`-log_(e)(a-x)=kt-log_(e)a`
या `kt=log_(e)a-log_(e)(a-x)`
या `kt=log_(e)""(a)/(a-x)`
या `k=(1)/(t)log_(e)""(a)/(a-x)`
या `k=(2.303)/(t)log_(10)""(a)/(a-x)`
समीकरण (3) को प्रथम कोटि की अभिक्रिया का गतिक समीकरण कहा जाता है।
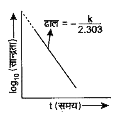
इस समीकरण की सहायता से k का मान ज्ञात कर सकते है। स्थिर ताप पर k का मान स्थिर रहता है। k का मात्रक `"सेकण्ड"^(-1)` या `"मिनट"^(-1)` है। .इस k का मान संलग्न में दर्शाये गए वक्र का ढाल `=-(k)/(2.303)` की सहायता से ज्ञात करते है। इस कोटि की अभिक्रिया में, स्थिर ताप पर किसी निश्चित अभिक्रिया के लिए k का मान सदैव स्थिर रहता है।
प्रथम कोटि की अभिक्रिया के लक्षण
(i) उपर्युक्त समीकरण (3) में यदि `t=t_(1//2)` (अर्द्धाआयुकाल)
तो `x=(a)/(2)` या `(a-x)=(a)/(2)`
`therefore k=(2.303)/(t_(1//2))log_(10)""(a)/(a//2)=(2.303)/(t_(1//2))log_(10)2`
`k=(2.303)/(t_(1//2))xx0.3010` या `t_(1//2)=(0.693)/(k)`
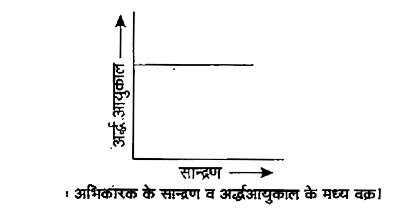
अतः स्पष्ट है कि प्रथम कोटि की अभिक्रिया का अर्द्धआयुकाल उसके अभिकारक के सान्द्रण पर निर्भर नहीं करता है।
(ii) प्रथम कोटि की अभिक्रिया में अभिकारक का सान्द्रण परिवर्तित करने पर उसका वेग स्थिरांक अपरिवर्तित रहता है। अतः प्रथम कोटि की अभिक्रिया में वेग स्थिरांक अभिकारक के सान्द्रण पर निर्भर नहीं करता है, जैसे-
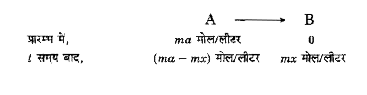
वेग स्थिरांक, `k=(2.303)/(t)log_(10)""(ma)/(ma-mx)`
`k=(2.303)/(t)log_(10)""(a)/((a-x))`
अतः अभिकारक का सान्द्रण परिवर्तन पर वेग स्थिरांक (k) का मान अपरिवर्तित रहता है।
(iii) प्रथम कोटि की अभिक्रिया के पूर्ण होम में अनन्त समय लगता है। अतः ये कभी पूर्ण नहीं होती है।
(iv) प्रथम कोटि की अभिक्रिया का वेग स्थिरांक, अभिकारक के सान्द्रण के मात्रक पर निर्भर नहीं होता है, बल्कि समय के मात्रक पर निर्भर करता है।