शून्य कोटि की अभिक्रिया-वह अभिक्रिया जिसकी प्रगति में अभिकारक के किसी भी अणु का सान्द्रण परिवर्तित नहीं होता है अर्थात अभिक्रिया का वेग अभिकारक के सान्द्रण पर निर्भर नहीं करता है, शून्य कोटि की अभिक्रिया कहलाती है-
माना कि कोई अभिक्रिया निम्नलिखित प्रकार से होती है-
`ArarrB+C`
यदि इसका वेग `prop[A]^(0)` हो तो शून्य कोटि की अभिक्रिया होगी।
उदाहरण-(1) सूर्य के प्रकाश की उपस्थिति में `H_(2)` व `Cl_(2)` का संयोग-
`H_(2)+Cl_(2)overset("सूर्य का प्रकाश")rarr2HCl`
(2) प्लैटिनम की उपस्थिति में `NH_(3)` का विघटन-
`2NH_(3)(g)underset("उत्प्रेरक")overset(Pt)rarrN_(2)(g)+3H_(2)(g)`
गतिक समीकरण- माना कि कोई शून्य कोटि की अभिक्रिया निम्नलिखित प्रकार से होती है-
`ArarrB+C`
तो शून्य कोटि की परिभाषा के अनुसार,
अभिक्रिया का वेग, `((dx)/(dt))prop[A]^(0)`
या `(dx)/(dt)=k[A]^(0)`
जहाँ `krarr` शून्य कोटि की अभिक्रिया का वेग स्थिरांक है तथा [A] अभिकारक का सान्द्रण है।
`therefore (dx)/(dt)=k` ...(1)
यदि अभिक्रिया के वेग तथा समय के मध्य वक्र खींचा जाए तो समय के अक्ष के समान्तर एक सीधी रेखा प्राप्त होती है।
अतः शून्य कोटि की अभिक्रिया का वेग स्थिरांक उस अभिक्रिया के वेग के बराबर होता है।
समीकरण (1) को निम्नलिखित प्रकार से लिखने पर,
`dx=k,dt`
समाकलन से, `intdx=kintdt`
या `x=kt+C`
जहाँ .C. समाकलन स्थिरांक है।
`t=0` पर `x=0` समीकरण (2) से,
`therefore C=0` अतः `x=kt`
या `k=(x)/(t)`
समीकरण (3) को शून्य कोटि की अभिक्रिया का गतिक समीकरण कहते है। इससे k का मान ज्ञात करते है। इसका मात्रक मोल `"लीटर"^(-1)" सेकण्ड"^(-1)` होता है।
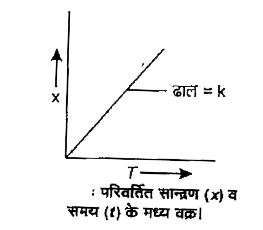
यदि x व t के मध्य वक्र खींचा जाए तो ढाल शून्य कोटि के वेग स्थिरांक का मान व्यक्त करती है।

शून्य कोटि की अभिक्रिया के गतिक समीकरण का प्रमुख अभिलक्षणिक गुण निम्नलिखित है-
(i) यदि `t=t_(1//2)` (अर्द्ध-आयुकाल) हो
तो `x=(a)/(2)` (जहाँ `ararr` अभिकारक का प्रारम्भिक सान्द्रण है)
`therefore k=(a//2)/(t_(1//2))`
या `t_(1//2)=(a)/(2k)` या `t_(1//2)propa`
अतः शून्य कोटि की अभिक्रिया का अर्द्ध-आयुकाल उसके प्रारम्भिक सान्द्रण के समानुपाती होता है अर्थात प्रारम्भिक सान्द्रण पर निर्भर करता है।
(ii) शून्य कोटि की अभिक्रिया में अभिक्रिया का वेग सदैव स्थिर रहता है तथा इसका मान अभिक्रिया के वेग स्थिरांक के समान होता है।
(iii) शून्य कोटि की अभिक्रिया सदैव पूर्ण होती है तथा इसके पूर्ण होने में लगा समय `a//k` होता है, जहाँ `ararr` अभिकारक का प्रारम्भिक सान्द्रण है।
(iv) शून्य कोटि की अभिक्रिया के वेग स्थिरांक का मात्रक अभिक्रिया के वेग के समान होता है।