Home
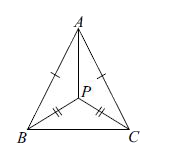
Class 9
MATHS
In the given figure, Delta ABC and Delta...

In the given figure, `Delta ABC and Delta PBC` are two isosceles triangles on the same base BC and vertices A and P are on the same side of BC. If A and P are joined, then

A

`angle BPA = (1)/(2) angle BAC`

B

`angle BAP = (1)/(2) angle BAC`

C

`angle CPA = (1)/(2) angle BAC`

D

`angle BAP =2 angel BAC`

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • IMO QUESTION PAPER 2018 SET A

    SCIENCE OLYMPIAD FOUNDATION |Exercise EVERYDAY MATHEMATICS|10 Videos

  • IMO QUESTION PAPER 2018 SET A

    SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION|5 Videos

  • IMO QUESTION PAPER 2017 SET B

    SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION|5 Videos

  • IMO QUESTION PAPER 2018 SET B

    SCIENCE OLYMPIAD FOUNDATION |Exercise Achievers Section |5 Videos

Similar Questions

Explore conceptually related problems

Delta ABC and Delta DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that (i) DeltaABD ~=DeltaACD (ii) DeltaABE~=DeltaACE (iii) AE bisects angleA as well as angleD (iv) AE is the perpendicualr bisector of BC.

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABD~=DeltaACD

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABP~=DeltaACP

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that AP bisects angleA as well as angleD .

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that : (i) DeltaABD cong DeltaACD (ii) DeltaABP cong DeltaACP (iii) AP bisects angleA as well as angleD (iv) AP is the perpendicular bisector of BC.

△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D . (iv) AP is the perpendicular bisector of BC.

In Figure,ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that /_ABD=/_ACD

ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that /_A B D\ =/_A C D

triangle ABC and triangle DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles