A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SCIENCE OLYMPIAD FOUNDATION -IMO QUESTION PAPER 2017 SET A-Achievers Section
- Match the following. {:(,"Column-I",,"Column-II"),(P.,"If points (k...
Text Solution
|
- State 'T' for true and 'F' for false and select the correct option. ...
Text Solution
|
- V(1),V(2),V(3) and V(4) are the volumes of four cubes of side lengths ...
Text Solution
|
- T F is a tower with F on the ground. The angle of elevation of T fr...
Text Solution
|
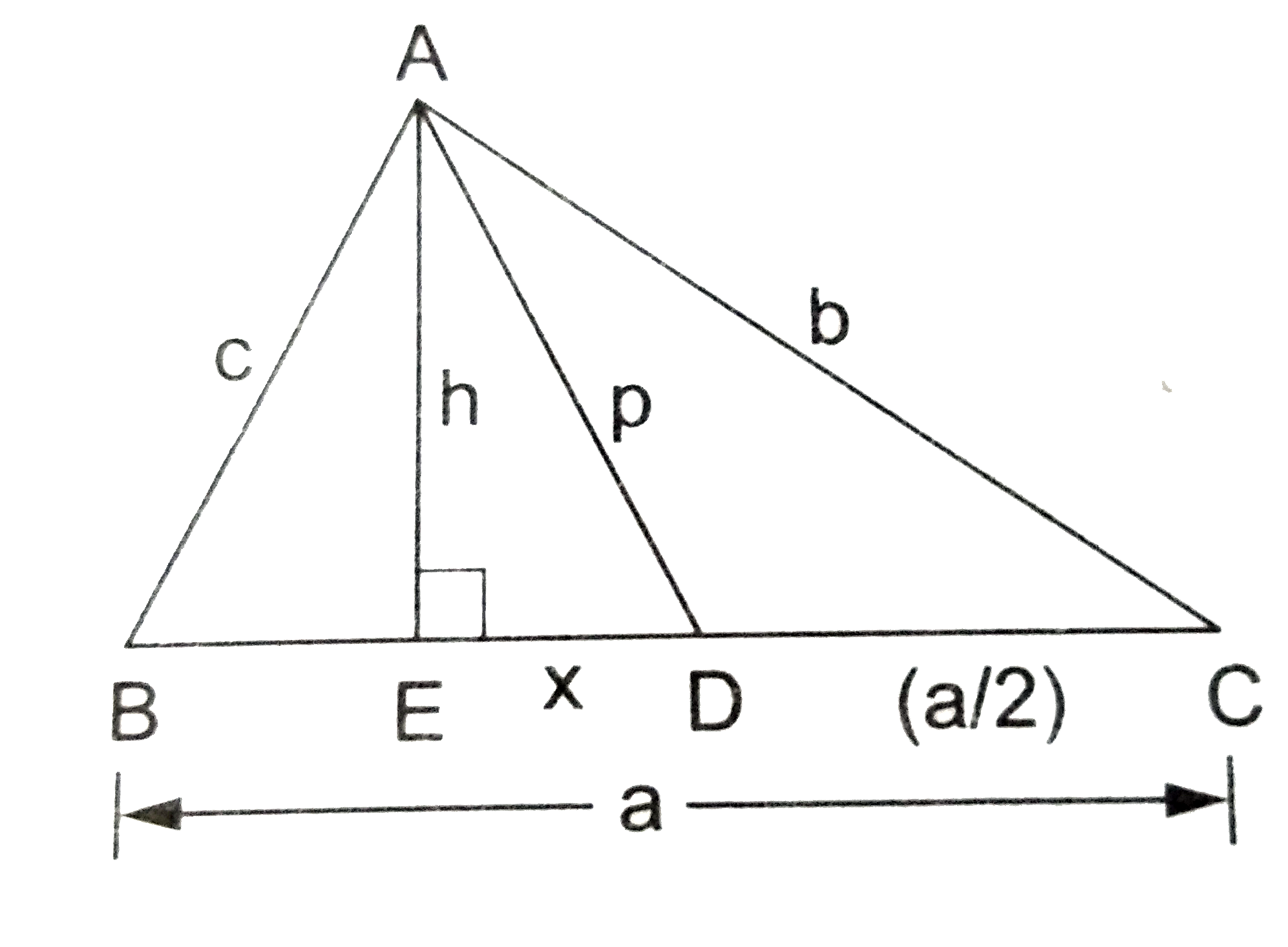
- In the given figure, D is the midpoint of side BC and AE bot BC. If BC...
Text Solution
|