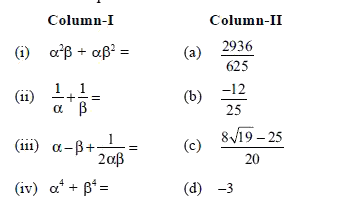A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SCIENCE OLYMPIAD FOUNDATION -IMO QUESTION PAPER 2019 SET A-Achievers section
- Which of the following options is incorrect ?
Text Solution
|
- Read the given statements carefully and select the correct option. S...
Text Solution
|
- If alpha and beta are the zeroes of the quadratic polynomial f(x)=5x^(...
Text Solution
|
- Read the given statements carefully and state 'T' for true and 'F' for...
Text Solution
|
- A die is thrown twice. What is the probability that (i) a multiple o...
Text Solution
|