A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
IMO QUESTION PAPER 2020 SET 1
SCIENCE OLYMPIAD FOUNDATION |Exercise Everyday Mathematics|10 VideosIMO QUESTION PAPER 2020 SET 1
SCIENCE OLYMPIAD FOUNDATION |Exercise Achievers Section|5 VideosIMO QUESTION PAPER 2019 SET B
SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION |5 VideosIMO QUESTION PAPER 2020 SET 2
SCIENCE OLYMPIAD FOUNDATION |Exercise Achievers Section|4 Videos
Similar Questions
Explore conceptually related problems
SCIENCE OLYMPIAD FOUNDATION -IMO QUESTION PAPER 2020 SET 1-Achievers Section
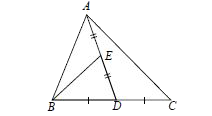
- ABC is a triangle in which E is the mid point of AD. Then, ar(DeltaBED...
Text Solution
|
- Select the incorrect option.
Text Solution
|
- Solve the following questions. (i) A vertical tower stands on a hori...
Text Solution
|
- Fill in the blanks and select the correct option. (i) The point on t...
Text Solution
|
- Match the following and select the correct option.
Text Solution
|
- Read the statements carefully and sate T for true and F for false. (...
Text Solution
|