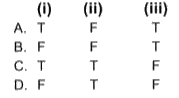Home
Class 10
MATHS
Read the given statements carefully and ...

Read the given statements carefully and state T for true and F for false.
(i) The value of k for which the equations x + 2y = 5 and 3x + ky - 15 = 0 has no solution, is 6.
(ii) The system of equations 3x - 5y = 20 and 6x - 10y = 40 has infinitely many solutions.
(iii) If the sum of the digits of a two digit number is 8 and difference between the number and the number formed by reversing the digits is 18, then the number is 34.

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020

    SCIENCE OLYMPIAD FOUNDATION |Exercise LOGICAL REASONING |1 Videos

  • SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020

    SCIENCE OLYMPIAD FOUNDATION |Exercise EVERYDAY MATHEMATICS |10 Videos

  • SAMPLE PAPER 4 (CLASS 10)

    SCIENCE OLYMPIAD FOUNDATION |Exercise Section E - Logical Reasoning |1 Videos

  • SOME APPLICATIONS OF TRIGONOMETRY

    SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION (HOTS)|5 Videos

Similar Questions

Explore conceptually related problems

The value of k for which the system of equations x+y -4 = 0 and 2x + ky = 3 has no solution, is:

Value of k for which system of equations kx + 2y = 5, 3x + y =1 has unique solution is

Find the value of k in which the system of equations kx + 2y = 5 and 3x + y = 1 has no solution ?

Find the value of k for which the system of equations kx - y = 2, 6x - 2y = 4 has infinitely many solutions

What is the value of k for which the system of equations x + 2y - 3 = 0 and 5x + ky + 7= 0 has no solution ?

For what value of k, the system of equations 8x + 5y = 9 and kx + 10y = 18 has infinitely many solutions?

The value of k, for which the system of equations 3x -ky-20 = 0 and 6x - 10y + 40 = 0 has no solution, is

Evaluate for what value of k the system of equations 2x - y = 5 and 6x + ky = 15 has infinitely many solutions.

For what value of k, the system of equation 8x + 5y = 9 and kx + 10y = 18 has infinite many solutions.

Find the value of k for which the system of equations 2x + ky = 1 and 3x - 5y = 7 has a unique solution.