A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SCIENCE OLYMPIAD FOUNDATION -STRUCTURE OF ATOM-ACHIEVERS SECTION (HOTS)
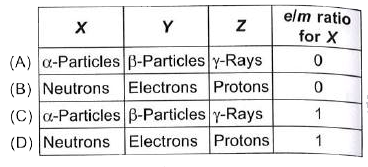
- Three invisible radiations X, Y and Z are passed through an electric f...
Text Solution
|
- A compound of carbon, hydrogen and nitrogen contains these elements in...
Text Solution
|
- Which of the given pairs of atoms contain(s) the same number of neutro...
Text Solution
|
- Description of a few hypothetical atoms is given in the table. ...
Text Solution
|
- Study the given mass spectrum of magnesium carefully. The numbe...
Text Solution
|
- Electron distribution of two elements P and Q in their outermost shell...
Text Solution
|