Home
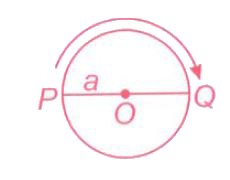
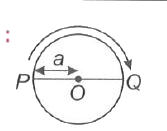
Class 6
PHYSICS
A cyclist moves from a certain point P a...

A cyclist moves from a certain point P and goes round a circle of radius a and reaches Q, exactly at the other side of the point P as shown in figure. The displacement of the cyclist would be

A

`pi a `

B

`2 pi a `

C

`2a `

D

`2pi//a`

Text Solution

Verified by Experts

The correct Answer is:
C

Displacement of the cyclist = Shortest distance between P and Q = PO+ OQ = a + a = 2a
Promotional Banner

Topper's Solved these Questions

  • MOTION AND MEASUREMENT OF DISTANCES

    SCIENCE OLYMPIAD FOUNDATION |Exercise ARCHIEVERS SECTION (HOTS) |4 Videos

  • LIGHT, SHADOWS AND REFLECTIONS

    SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION (HOTS)|5 Videos

  • NSO MODEL TEST PAPER 01

    SCIENCE OLYMPIAD FOUNDATION |Exercise ACHIEVERS SECTION|2 Videos

Similar Questions

Explore conceptually related problems

A cyclist moves from a certain point X and goes round a circle of radius 'r' and reaches Y, exactly at the other side of the point X, as shown in Fig. 2.9. The displacement of the cyclist would be

The net resistance between points P and Q in the circuit shown in figure is

Draw a circle of radius 3 cm. Take a point P on the circle. At point P, construct a tangent to the circle.

Four girls skating on circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in figure. For which girls displacement is equal to the actual length of path ?

The equivalent capacitance between points P and Q of the combination shown in figure is

Six metallic plated each with a surface area of one side A. are placed at a distanced d from each other. The alternate plates are connected to points P and Q as shown in figure : The capacitance of the system is :

P, Q are the points on the circle. The part of the circle, PQ is called ________ of the circle.

Perpendiculars are drawn,respectively,from the points P and Q to the chords of contact of the points Q and P with respect to a circle. Prove that the ratio of the length of perpendiculars is equal to the ratio of the distances of the points P and Q from the center of the circles.