Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
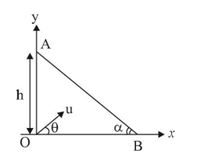
- In the adjacent figure AB is an inclined wall making an angle alpha =...
Text Solution
|
- A stone is projected from the ground with velocity 50(m)/(s) at an ang...
Text Solution
|
- A stone is projected from point A with speed u making an angle 60^@ wi...
Text Solution
|
- A body projected from a point O at an angle theta , just crosses a wal...
Text Solution
|
- A particle is projected from the ground at an angle of 60^(@) with hor...
Text Solution
|
- पत्थर के एक टुकड़े को क्षैतिज से 60^(@) कोण पर 40 मी/से के वेग से फेंक...
Text Solution
|
- जमीन से एक पत्थर को 25 मी/से के वेग से प्रक्षेपित किया गया है | दो सेक...
Text Solution
|
- 50 मी/से के वेग से एक पत्थर को 30^(@) के कोण पर प्रक्षेपित किया गया ह...
Text Solution
|
- A stone is projected from the ground with a velocity of 20 m/s at angl...
Text Solution
|