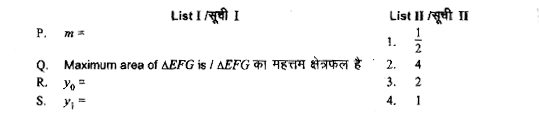A
B
C
D
लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
JEE ADVANCED पेपर - 2 (2013)
JEE Main & Advanced (Hindi Medium)|Exercise PART III : MATHEMATICS (खण्ड -2) (अनुच्छेद प्रकार) |8 VideosJEE ADVANCED पेपर - 2 (2012)
JEE Main & Advanced (Hindi Medium)|Exercise भाग - III : गणित खंड - III : बहुल सही उत्तर प्रकार|6 VideosJEE ADVANCED पेपर - 2 (2014)
JEE Main & Advanced (Hindi Medium)|Exercise PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )|4 Videos
JEE Main & Advanced (Hindi Medium)-JEE ADVANCED पेपर - 2 (2013)-PART III : MATHEMATICS (खण्ड - 3) (सुमेलन सूची प्रकार)
- सूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिए गए कोड का प...
Text Solution
|
- एक रेखा L:y = mx + 3,y - अक्ष के बिन्दु E(0,3) तथा परवलय के चाप y^2 = ...
Text Solution
|
- सूची - I को सूची – II से सुमेलित कीजिए तथा सूचियों के नीचे दिए गए कोड ...
Text Solution
|
- रेखाएँ L1 : (x-1)/2=y/(-1)=(z+3)/1,L2:(x-4)/(1)=(y+3)/1=(z+3)/2 तथा ...
Text Solution
|