Home
Class 11
PHYSICS
The spectrum of a black body at two temp...

The spectrum of a black body at two temperatures `27^(@)C` and `327^(@)C` is shown in the figure. Let `A_(1)` and `A_(2)` be the areas under the two curves respectively. Find the value of `(A_(2))/(A_(1))`

A

`1:16`

B

`4:1`

C

`2:1`

D

`16:1`

Text Solution

Verified by Experts

The correct Answer is:
D
Area under given curve `prop T^4`
`implies (A_2)/(A_1)=(T_2^4)/(T_1^4)=((273+327)/(273+27))^4 implies (A_2)/(A_1)=(16)/(1)`
Promotional Banner

Topper's Solved these Questions

  • TRANSMISSION OF HEAT

    ERRORLESS|Exercise NCERT BASED QUESTIONS (Radiation (Wien.s law))|13 Videos

  • TRANSMISSION OF HEAT

    ERRORLESS|Exercise NCERT BASED QUESTIONS (Radiation (Stefan.s law))|25 Videos

  • TRANSMISSION OF HEAT

    ERRORLESS|Exercise NCERT BASED QUESTIONS (Convection)|4 Videos

  • THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY

    ERRORLESS|Exercise ASSERTION & REASON|10 Videos

  • UNITS, DIMENSIONS AND MEASUREMENT

    ERRORLESS|Exercise ASSERTION & REASON |17 Videos

Similar Questions

Explore conceptually related problems

The spectra of a black body at temperatures 273^(@)C and 546^(@)C are shown in the figure. If A_(1) and A_(2) be area under the two curves respectively, the value of (A_(2))/(A_(1)) is

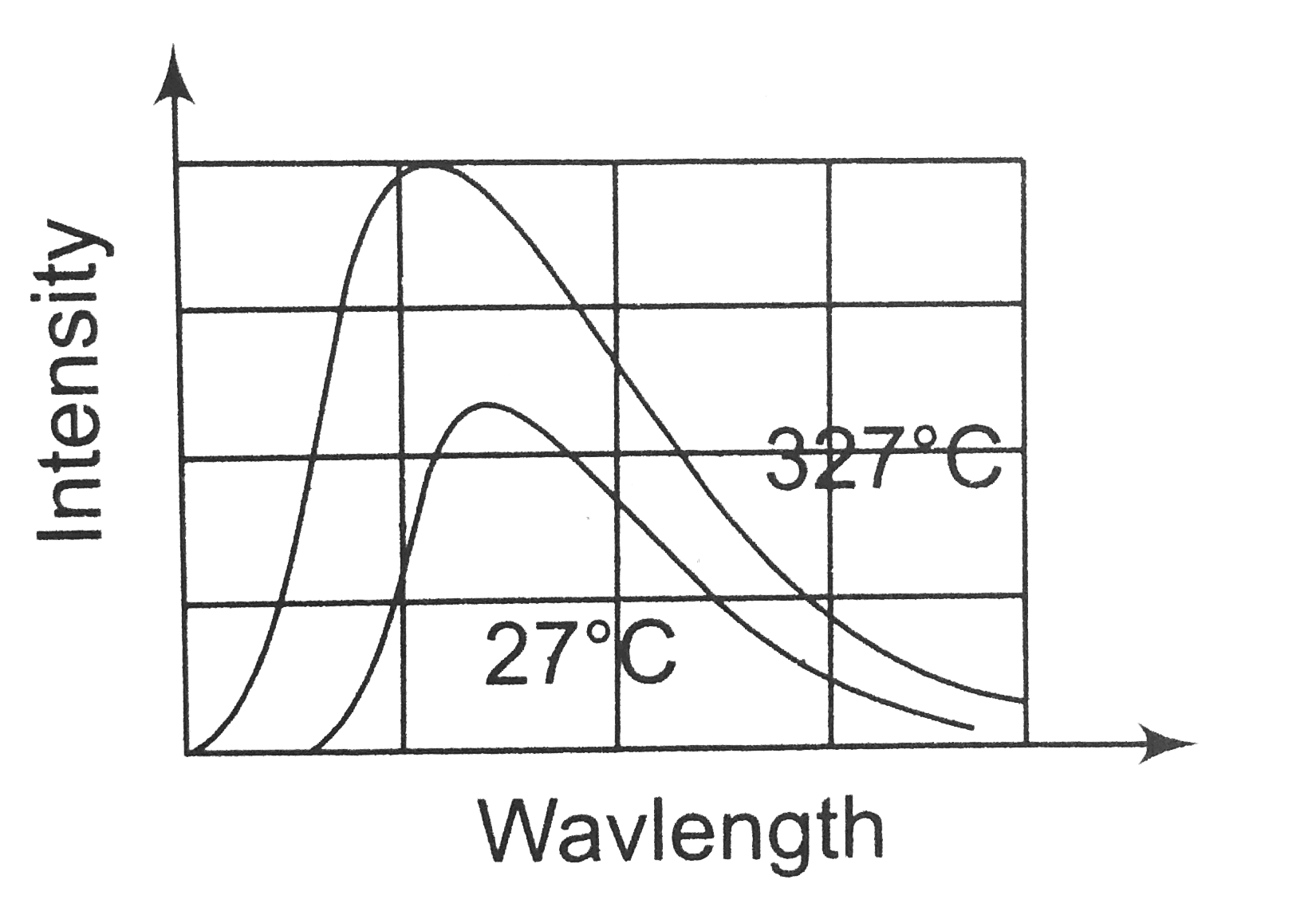
The specturm of a black body at two temperatures 27^(@)C and 327^(@)C is show in the Fig. 7(e).20 . Let A_(1) and A_(2) be the respective areas tunder the two curved. Estimate the ratio A_(2)//A_(1) .

If a_(1),a_(2),a_(3) are the last three digits of 17^(256) respectively then the value of a_(2)-a_(1)-a_(3) is equal

In the figure shown the readings of the ammeters A_(1) and A_(2) are respectively.

A regular pentagons is inscribed in a circle. If A_(1) and A_(2) represents the area of circle and that of regular pentagon respectively, then A_(1) : A_(2) is

If the area of the circle is A_(1) and the area of the regular pentagon inscribed in the circle is A_(2), then find the ratio (A_(1))/(A_(2)) .

Let ABC and AB'C be two non-congruent triangles with sides BC=B'C=5, AC=6, and angleA is fixed. If A_(1) and A_(2) are the area of the two triangles ABC and AB'C, then the value of (A_(1)^(2)+A_(2)^(2)-2A_(1)A_(2)cos 2A)/((A_(1)+A_(2))^(2)) is

Let a and b be two positive real numbers such that a+2b<=1. Let A_(1) and A_(2) be, respectively,the areas of circles with radii ab^(3) and b^(2). Then the maximum possible value of (A_(1))/(A_(2)) is:

If a_(1) and a_(2) aare two non- collineaar unit vectors and if |a_(1)+a_(2)|=sqrt(3), ,then value of (a_(1)-a_(2)).(2a_(1)-a_(2)) is