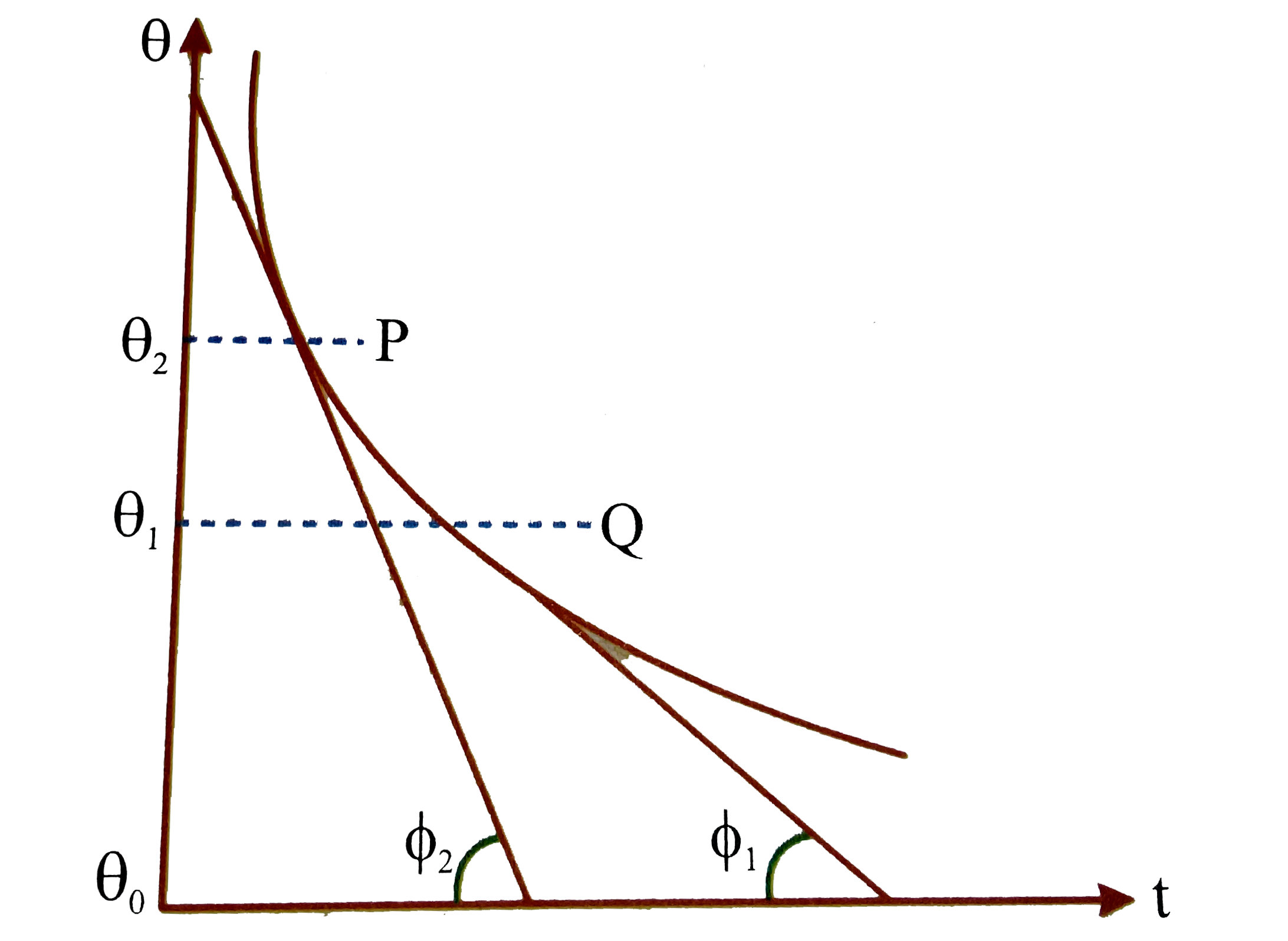
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
TRANSMISSION OF HEAT
ERRORLESS|Exercise PAST YEARS QUESTIONS|21 VideosTRANSMISSION OF HEAT
ERRORLESS|Exercise Assertion & Reason|22 VideosTRANSMISSION OF HEAT
ERRORLESS|Exercise NCERT BASED QUESTIONS (Radiation (Stefan.s law))|25 VideosTHERMOMETRY, THERMAL EXPANSION AND CALORIMETRY
ERRORLESS|Exercise ASSERTION & REASON|10 VideosUNITS, DIMENSIONS AND MEASUREMENT
ERRORLESS|Exercise ASSERTION & REASON |17 Videos
Similar Questions
Explore conceptually related problems
ERRORLESS-TRANSMISSION OF HEAT -NCERT BASED QUESTIONS (Radiation (Newton.s Law of Cooling))
- Newton's law of cooling is a special case of .
Text Solution
|
- A bucket full of hot water cools from 75^(@)C to 70^(@)C in time T(1),...
Text Solution
|
- A cane is taken out from a refrigerator at 0^(@)"C". The atmospheric t...
Text Solution
|
- A body takes 5 minutes to cool from 90^(@)C to 60^(@)C . If the temper...
Text Solution
|
- If a metallic sphere gets cooled from 62^(@)C to 50^(@)C in utesmin1...
Text Solution
|
- A body cools from 60^(@)C to 50^(@)C in 10 minutes . If the room tempe...
Text Solution
|
- For a small temperature difference between the body and the surroundin...
Text Solution
|
- A calorimeter of mass 0.2 kg and specific heat 900 J//kg-K. Containing...
Text Solution
|
- Two spheres of radii in the ratio 1 : 2 and densities in the ratio 2 :...
Text Solution
|
- A body cools in a surrounding which is at constant temperature of thet...
Text Solution
|
- A sphere a cube and a thin ciruclar plate all of same material having ...
Text Solution
|