A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Acceleration Due to Gravity)|39 VideosGRAVITATION
ERRORLESS|Exercise NCERT BASED QUESTIONS (Gravitation Potential, Energy and Escape Velocity)|38 VideosFRICTION
ERRORLESS|Exercise ASSERTION & REASON |8 VideosKINETIC THEORY OF GASES
ERRORLESS|Exercise ASSERTION AND REASON |16 Videos
Similar Questions
Explore conceptually related problems
ERRORLESS-GRAVITATION-Assertion and Reason
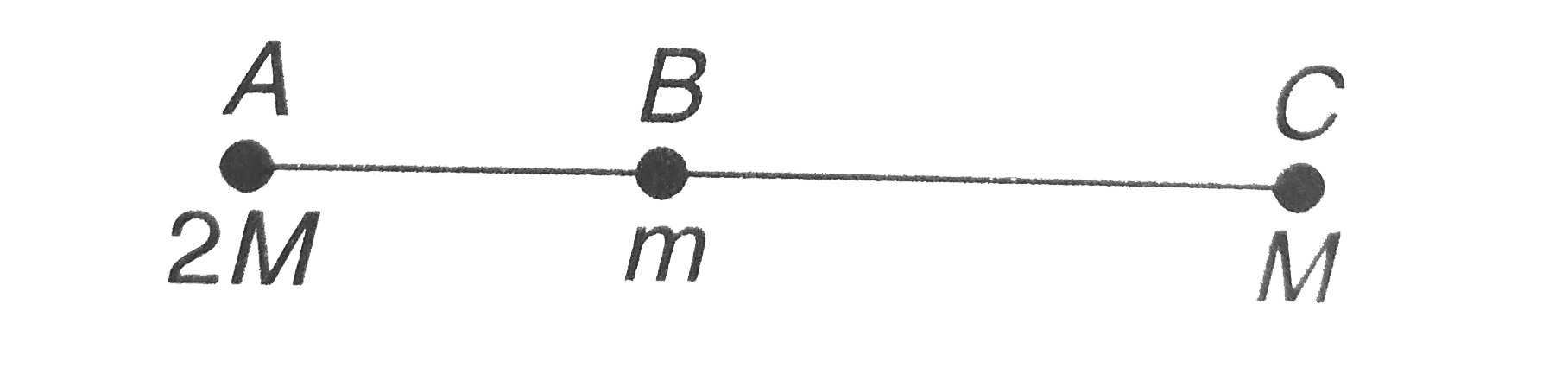
- particles of masses 2M m and M are resectively at points A , B and C w...
Text Solution
|
- Statement I: The smaller the orbit of a planet around the Sun, the sho...
Text Solution
|
- Statement -1: Gravitational force between two particles is negligibly ...
Text Solution
|
- Assertion: There is no effect of rotation of a earth on acceleration d...
Text Solution
|
- Assertion : We can not move even a finger without disturbing all the s...
Text Solution
|
- Assertion : If a pendulum falls freely, then its time period becomes i...
Text Solution
|
- Statement I: If the earth suddenly stops rotating about its axis, then...
Text Solution
|
- Assertion : The difference in the value of acceleration due to gravity...
Text Solution
|
- Assertion: For the plantes orbiting around the sun, angular speed, lin...
Text Solution
|
- Assertion : A force act upon the earth revolving in a circular orbit...
Text Solution
|
- Assertion: The speed of revolution of an artificial satellite revoving...
Text Solution
|
- Assertion : Gravitational potential of earth at every place on it is...
Text Solution
|
- Assertion : Even when orbit of a satellite is elliptical, its plane of...
Text Solution
|
- Assertion : A planet moves faster, when it is closer to the sun in i...
Text Solution
|
- Assertion : Orbital velocity of a satellite is greater than its esca...
Text Solution
|
- Assertion : The speed of satellite always remains constant in an orb...
Text Solution
|
- Assertion : Earth has an atmosphere but the moon does not. Reason ...
Text Solution
|
- Assertion: The time period of geostationary satellite is 24 hrs. Rea...
Text Solution
|
- Assertion : The principle of superposition is not valid for gravitat...
Text Solution
|
- Assertion: Two different planets have same escape velocity. Reason:...
Text Solution
|
- Assertion: The time period of revolution of a satellite close to surfa...
Text Solution
|