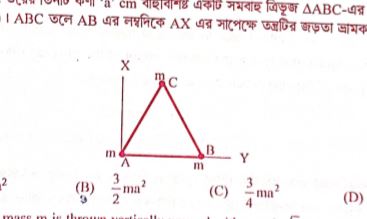
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three particles, each of mass 'm' grams situated at the vertices of an...
Text Solution
|
- Three particles, each of mass m are situated at the vertices of an equ...
Text Solution
|
- Three particles, each of mass m grams situated at the vertices of an e...
Text Solution
|
- समान द्रव्यमान m के तीन कण L भुजा वाली समबाहु त्रिभुज ABC के तीन कोनों...
Text Solution
|
- चित्र 16.13 में समान द्रव्यमान m के तीन कण, L भुजा वाले समबाहु त्रिभुज...
Text Solution
|
- Three particles each of 'm' are kept at the three vertices of an equil...
Text Solution
|
- Three particles each of mass 100 g are placed at the vertices of an eq...
Text Solution
|
- m द्रव्यमान के तीन कण l सेमी भुजा के समबाहु त्रिभुज के शीर्षों पर स्थि...
Text Solution
|
- Three particles, each of mass m are situated at the vertices of an equ...
Text Solution
|