Topper's Solved these Questions
QUESTION PAPER 2022 TERM 2 SET 2 STANDARD
X BOARDS|Exercise SECTION C|7 VideosQUESTION PAPER 2022 TERM 2 SET 2 STANDARD
X BOARDS|Exercise SECTION C|7 VideosQUESTION PAPER 2022 TERM 2 SET 1 STANDARD
X BOARDS|Exercise QUESTION|18 VideosQUESTION PAPER 2022 TERM 2 SET 3 STANDARD
X BOARDS|Exercise SECTION C|7 Videos
Similar Questions
Explore conceptually related problems
X BOARDS-QUESTION PAPER 2022 TERM 2 SET 2 STANDARD-SECTION B
- The frequency distribution given below shows the weight of 40 students...
Text Solution
|
- Draw a circle of radius 4 cm. Construct a pair of tangents to the circ...
Text Solution
|
- Draw a line segment PQ = 7.5 cm. Divide it in the ratio 3: 1.
Text Solution
|
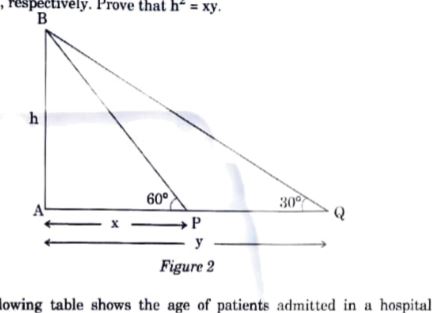
- In Figure, the angles of elevation of the top of a tower AB of height ...
Text Solution
|
- The following table shows the age of patients admitted in a hospital d...
Text Solution
|