Home
Class 12
MATHS
In a game of Archery, each ring of the A...

In a game of Archery, each ring of the Archery target is valued. The centremost ring is worth 10 points and rest of the rings are allotted points 9 to 1 in sequential order moving outwards.
Archer A is likely to earn 10 points with a probability of 0.8 and Archer B is likely the earn 10 points with a probability of 0.9.

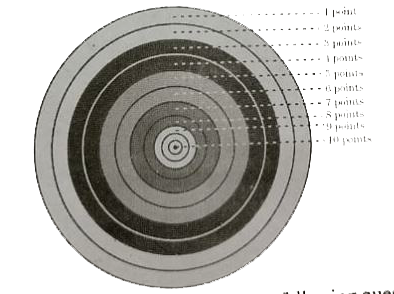
Based on the above information, answer the following questions :
If both of them hit the Archery target, then find the probability that
exactly one of them earns 10 points.

Promotional Banner

Topper's Solved these Questions

  • QUESTION PAPER 2022 TERM 2 SET 2

    XII BOARDS PREVIOUS YEAR|Exercise Section - C|4 Videos

  • QUESTION PAPER 2022 TERM 2 SET 1

    XII BOARDS PREVIOUS YEAR|Exercise SECTION C|6 Videos

  • QUESTION PAPER 2022 TERM 2 SET 3

    XII BOARDS PREVIOUS YEAR|Exercise SECTION C (CASE-STUDY BASED QUESTION)|1 Videos

Similar Questions

Explore conceptually related problems

A and B stand in a ring with 10 other persons. If the arrangement of the persons is at random,then the probability that there are exactly 3 persons between A and B is

The probability that a bomb will hit a target is 0.8 Find the probability that out of 10 bombs dropped.exactly 4 will hit the target .

If the point (1,0),(0,1) and (x,8) are collinear, then the value of x is equal to

The probability of hitting a target in any shot is 0.2 If 10 shorts are fired , find the probability that the target will be hit at least twice. [ Given: (0.8)^9= 0. 1342]

The probability that a bomb will hit a target is 0.8. The probability that out of 10 bombs dropped, exactly 2 will miss the target is

A ring of radius R is charged uniformly with a charge +Q . The potential at a point on its axis at a distance 'r' from any point on ring will be-