Home
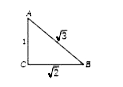
Class 11
PHYSICS
If hat(i), hat(j) and hat(k) represent u...

If `hat(i), hat(j)` and `hat(k)` represent unit vectors along the x, y and z axes respectively, then the angle `theta` between the vectors `(hat(i) + hat(j) + hat(k))` and `(hat(i) + hat(j))` is equal to :

A

`sin^(-1) ((1)/(sqrt3))`

B

`sin^(-1) (sqrt((2)/(3)))`

C

`cos^(-1) ((1)/(sqrt3))`

D

`90^(@)`

Text Solution

Verified by Experts

The correct Answer is:
A
Since `vec(A).vec(B)= AB cos theta`
`rArr cos theta= (vec(A).vec(B))/(AB)= ((hat(i) + hat(j) + hat(k))(hat(i) + hat(j)))/(sqrt(1^(2) + 1^(2) +1^(2)) sqrt(1^(2) + 1^(2)))`
`rArr cos theta= (2)/(sqrt6) = sqrt((2)/(3))`
`rArr sin theta= (1)/(sqrt3)`
`rArr theta= sin^(-1) ((1)/(sqrt3))`
Promotional Banner

Similar Questions

Explore conceptually related problems

If hat(i), hat(j) and hat(k) are unit vectors along x,y and z-axis respectively, the angle theta between the vector hat(i) + hat(j) + hat(k)" ""and vector" hat(j) is given by

Find the angle between the vectors hat(i)-hat(j) and hat(j)-hat(k) .

The angle between the vectors : vec(a)=hat(i)+2hat(j)-3hat(k) and 3hat(i)-hat(j)+2hat(k) is :

The angle between the vectors (hat i + hat j + hat k) and ( hat i - hat j -hat k) is

Find the angle between the vectors hat(i)+3hat(j)+7hat(k) and 7hat(i)-hat(j)+8hat(k) .

The angle between the vectors hat(i)-hat(j) and hat(j)+hat(k) is :

Angle between the vectors (hat(i)+hat(j)) and (hat(j)-hat(k)) is

Find the angle between the vectors : vec(a)=hat(i)+hat(j)-hat(k) " and " vec(b)=hat(i)-hat(j)+hat(k)

The angle between the Vector (hat(i)+hat(j)) and (hat(j)+hat(k)) is