Home
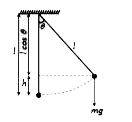
Class 11
PHYSICS
The angular amplitude of a simple pendul...

The angular amplitude of a simple pendulum is `theta_(0)`. The maximum tension in its string will be

A

`mg(1-theta_(0))`

B

`mg(1 + theta_(0))`

C

`mg(1- theta_(0)^(2))`

D

`mg(1 + theta_(0)^(2))`

Text Solution

Verified by Experts

The correct Answer is:
D
Maximum tension
`T = (mv_(B)^(2))/r + mg`
Since, `mgh = 1/2 mv_(B)^(2)`
`rArr v_(B)^(2) = 2gh = 2gl(1- cos theta_(0))`
`therefore T = mg + (2mgl)/l (1- cos theta_(0))`
`= mg + 2 mg xx 2 sin^(2) theta_(0)/2`
For small angle `sin theta = theta`
`T = mg + 4mg xx (theta_(0)/2)^(2) = mg (1 + theta_(0)^(2))`
Promotional Banner

Similar Questions

Explore conceptually related problems

The angular amplitude of a simple pendulum is theta_(0) . The maximum tension in the string is

Suppose the amplitude of a simple pendulum having a bob of mass m is theta_0 . Find the tension in the string when the bob is at its extreme position.

when the bob of a simple pendulum swings, the work done by tension in the string is :

The tension in the string of a simple pnedulum is

A simple pendulum oscillates with an anglular amplitude of theta . If the maximum tension in the string is 3 times the minimum tension, then the value of cos theta is

The velocity of simple pendulum is maximum at

The maximum tension in the string of an oscillating simple pendulum is 3% more than the minimum tension in the string. The angular amplitude of oscillations of the pendulum is

At what points along the path of a simple pendulum is the tension in the string maximum?

A simple pendulum with a bob of mass m swings with an angular amplitude of 40^@ . When its angular displacement is 20^@ , the tension in the string is greater than mg cos 20^@