Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ball is thrown from the ground into air. AT a height of 9.0 m, the ...
Text Solution
|
- A projectile is given an initial velocity of ( hat(i) + 2 hat (j) ) m/...
Text Solution
|
- A projectile is thrown with an initial velocity of v = a hat i + b hat...
Text Solution
|
- At a height 0.4 m from the ground the velocity of a projectile in vect...
Text Solution
|
- A ball is thrown from the ground into air. AT a height of 9.0 m, the ...
Text Solution
|
- एक गेंद 15 मीटर/सेकण्ड के वेग से क्षैतिज से 30^(@) का कोण बनाते हुए फ...
Text Solution
|
- A ball of mass 2 kg is thrown from a tall building with velocity, v=...
Text Solution
|
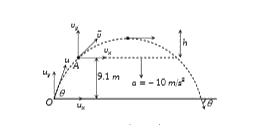
- A ball is shot from the ground into the air. At the height of 9.1 m, i...
Text Solution
|
- At t=0 a 1.0 kg ball is thrown from a tall tower with vec(v)=(18 m//s)...
Text Solution
|