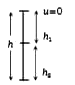A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A stone is dropped from a height h. Simultaneously, another stone is t...
Text Solution
|
- On the earth, a stone is thrown from a height in a direction parallel ...
Text Solution
|
- A stone is dropped from a height h simultaneously another stone is thr...
Text Solution
|
- A stone thrown vertically up from the ground reaches a maximum height ...
Text Solution
|
- A stone is dropped from a height h. Simultaneously, another stone is t...
Text Solution
|
- A stone is dropped from a height h. simultaneously, another stone is t...
Text Solution
|
- A stone is dropped from a height h. Simultaneously another stone is th...
Text Solution
|
- h উচ্চতা থেকে একটি পাথরকে নীচে ফেলা হল। একই সঙ্গে ভূমি থেকে একটি পাথরক...
Text Solution
|
- A stone is dropped from a height h. Another stone is thrown simultaneo...
Text Solution
|