Home
Class 11
PHYSICS
A particle starts from rest at t= 0 and...

A particle starts from rest at ` t= 0` and undergoes and acceleration (a) in `ms^(-2)` with time (t) in seconds which is shown in Fig. 2 (DF) .16 . Which one of the following plot represents velocity (v) (in `ms^(-1)`) verses time (in seconds ) ?

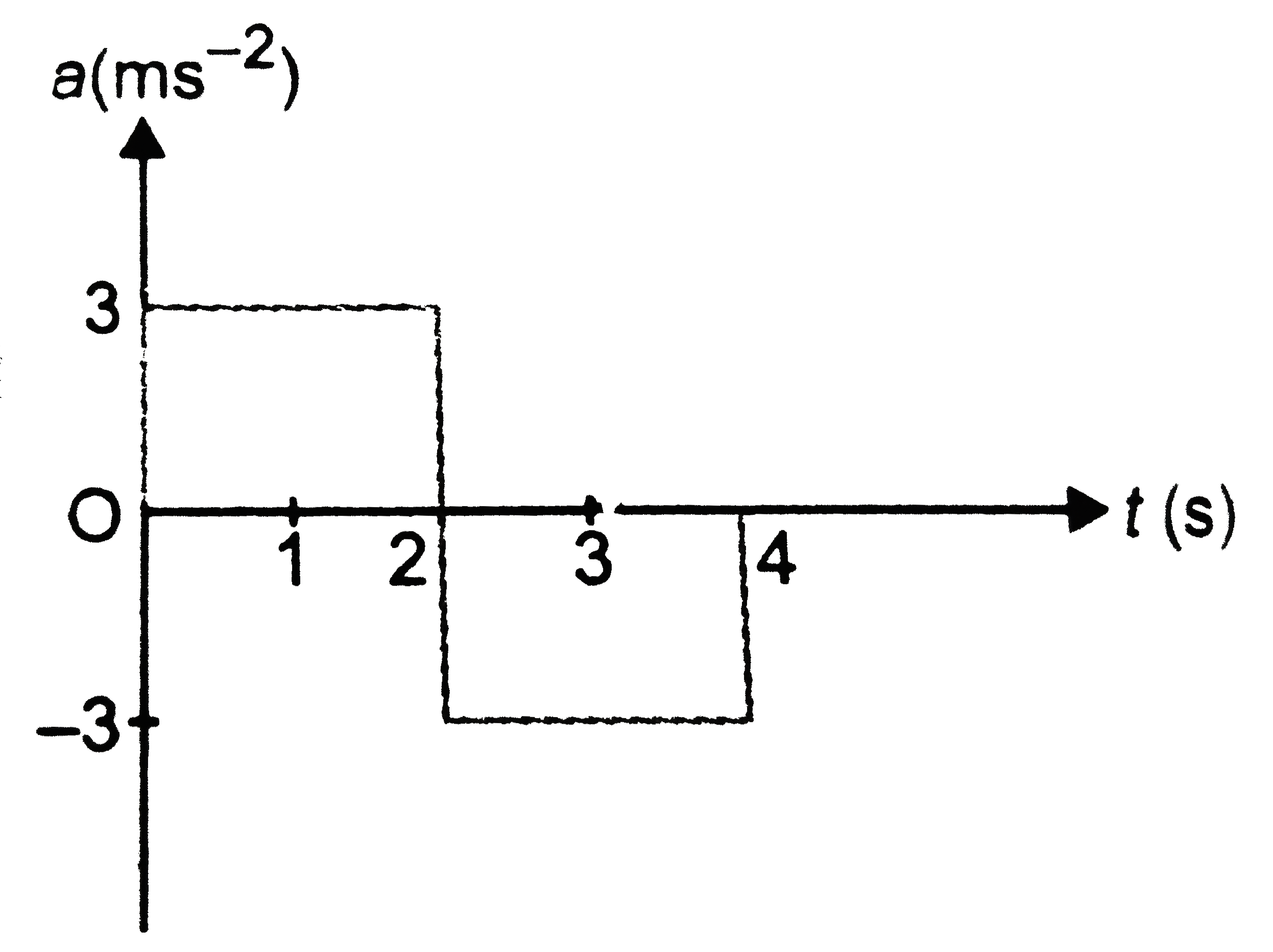
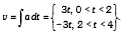A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A
t = 0 to 2 sec
u = 0`, a=3 m//s^2`
`rArr v = u + at = 3 xx2 = 6m//s`
Now, t = 2 to 4 second
`v = 6 - 3 xx 2 = 0m//s`
`a = 3, 0 lt t lt 2`
` = -3, 2 lt t lt 4`
Promotional Banner

Similar Questions

Explore conceptually related problems

A particle starts from rst at t= 0 and undergoes and acceleration (a) in ms^(-2) with tiem (t) in seconds which is shown in Fig. 2 (DF) .16 . Which one of the following plot repesents velocity (v) (in ms_1) versis time (in seconds ) ?

A particle starts from rest and undergoes an acceleration as shown in figure. The velocity-time graph from figure will have a shape.

A particle starts from rest at t=0 and undergoes an acceleration as shown in figure. Draw the velocity-time graph of the motion of the particle during the interval from zero to 4 second.

The distance travelled by a particle starting from rest and moving with an acceleration (4)/(3) ms^-2 , in the third second is.

The acceleration (a)-time(t) graph for a particle moving along a straight from rest is shown in figur. Which of the following graph is the best representation of its velocity (v) with time (t) ?

A particle starts from rest. Its acceleration at time t=0 is 5 m//s^(2) which varies with time as shown in the figure. The maximum speed of the particle will be

A particle starts from rest with a time varying acceleration a=(2t-4) . Here t is in second and a in m//s^(2) The velocity time graph of the particle is

A particle starts from rest with uniform acceleration a . Its velocity after n seconds is v . The displacement of the particle in the two seconds is :

A particle starts from rest and moves with acceleration a which varies with time t as a=kt where k is a costant. The displacement s of the particle at time t is

A particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure. The maximum speed of the particle will be.