Home
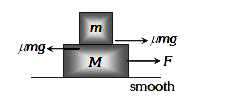
Class 11
PHYSICS
A mass m rests on another mass M. The co...

A mass m rests on another mass M. The co-efficient of static friction between the surfaces of m and M is `mu`. M rests on smooth frictionless horizontal plane. The maximum force applied horizontally on M for which m will move along with M without slipping is

A

mg + `mu` mg

B

`(M + m) mu g `

C

`(mM)/(M + m) "" mu g `

D

`mu mg`

Text Solution

Verified by Experts

The correct Answer is:
B
`ma_("max") = mu mg , " " therefore a_("max") = mu g`
`F_("max") - mu mg = Ma_("max")`
`therefore F_("max") = (m + M)mu g `
Promotional Banner

Similar Questions

Explore conceptually related problems

The coefficient of static friction between the two blocks shown in figure is mu and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

A block of mass m rests on a bracket of mass M. The coefficients of friction between block and bracket are mu_(s) and mu_(k) . The bracket rests on a frictionless surface. What is the maximum force F that can be applied if the block is not to slide on the bracket?

A small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is mu . The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?

A bar of mass m_(1) is placed on a plank of mass m_(2) which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t_(0) at which the plank starts sliding is :

A block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is mu and that of between lower blood from the horizontal surface is zero. A horizontal force F=4/3 mu mg is applied on the block of mass 2m . Acceleration of lower block is

A block of mass m is placed at rest on an inclination theta to the horizontal.If the coefficient of friction between the block and the plane is mu , then the total force the inclined plane exerts on the block is

A block of mass m is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is mu_(1) and that between the block of mass M and horizontal surfece is mu_(2) What maximum horizontal force can be applied to the lower block move without separation?

In figure-2.86, the blockA of mass M_(1) rests on a rough horizontal surface. The coefficient of friction between the block and the surface is mu . A uniform plank B, of mass M_(2) rests on A. B is prevented from moving by connecting it to a light rod R which is hinged at one end H.The coefficient of friction between A and B is mu . Findthe acceleration of blocks A and C. [(M_(3)g-mug(M_(1)+2M_(2)))/((M_(1)+M_(3)))]