Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
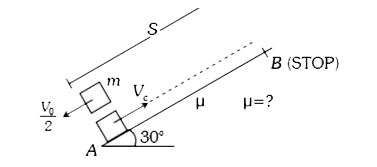
- A block starts moving up an inclined plane of inclination 30^@ with an...
Text Solution
|
- A block of mass m is projected up with a velocity v0 along an inclined...
Text Solution
|
- In figure, the angle of inclination of the inclined plane is 30^@ . Fi...
Text Solution
|
- (a) A block slides down an incline of angle 45^(@) with an acceleratio...
Text Solution
|
- An ice cube is kept on an inclined plane of angle 30^(@) . The coeffic...
Text Solution
|
- A block is released from the top of an inclined plane of inclination t...
Text Solution
|
- Block of mass 10 kg is moving on inclined plane with constant velocity...
Text Solution
|
- A block starts moving up an inclined plane of inclination 30^@ with an...
Text Solution
|
- A block is pushed up a rough inclined plane of 45^(@) with a velocity...
Text Solution
|