Home
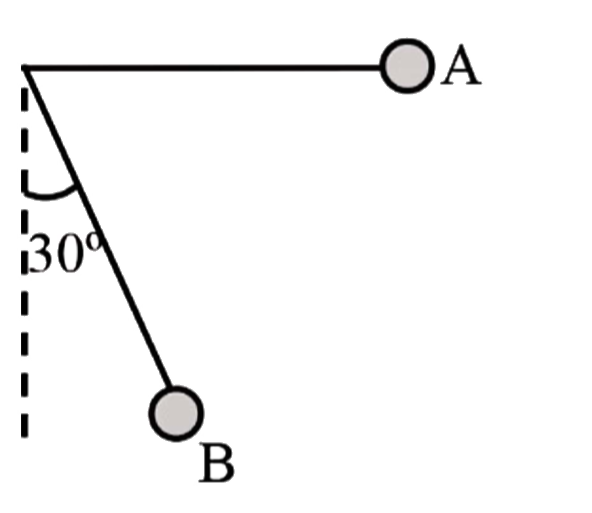
Class 11
PHYSICS
A simple pendulum is released from A as ...

A simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is

A

`(mgl)/2 `

B

`(mgl)/sqrt2 `

C

`sqrt3/2 mgl`

D

`2/sqrt3 mgl`

Text Solution

Verified by Experts

The correct Answer is:
C
`h= l cos 30^@ = (lsqrt3)/2`
`DeltaKE = mgh = (mglsqrt3)/2`
Promotional Banner

Similar Questions

Explore conceptually related problems

If the length of a simple pendulum is halved, then its energy becomes

The bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?

A simple pendulum of length 1m has bob of mass 100 g. It is displaced through an angle of 60^@ from the vertcal and then released. The kinetic energy of bob when it passes through the mean position is

The effictive length of a simple pendulum is the sum of the following three : length of string , radius of bob , and length of hook. In a simple pendulum experiment , the length of the string , as measured by a meter scale , is 92.0 cm . The radius of the bob combined with the length of the hook , as measured by a vernier callipers , is 2.15 cm . The effictive length of the pendulum is

If a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle theta with the horizontal.

The bob of a pendulum is released from a horizontal position. If the length of pendulum is 2 m, what is the speed with which the bob arrives at the lower most point. Assume that 10% of its energy is dissipated against air resistance. (Take g = 10 m s^(-2) )

Two identical simple pendulums A and B are fixed at same point. They are displaced by very small angles alpha " and " beta ( = 2 alpha) respectively and are simultaneously released from rest at time t = 0. Collisions between the pendulum bobs are elastic and length of each pendulum is l. (a) What is the minimum number of collisions between the bobs after which the pendulum B will again reach its original position from where it was released ? (b) Find the time (t) at which B reaches its initial position for the first time after the release. (c) Write the kinetic energy of pendulum B just after n^(th) collision? Take mass of each bob to be m.

Figure shows the kinetic energy K of a simple pendulum versus its angle theta from the verticle. The pendulum bob has mass 0.2 kg . If the length of the pendulum is equal to (n)/(g) meter. Then find n (g = 10 m//s^(2))

Kinetic energy of the bob of a simple pendulum is maximum