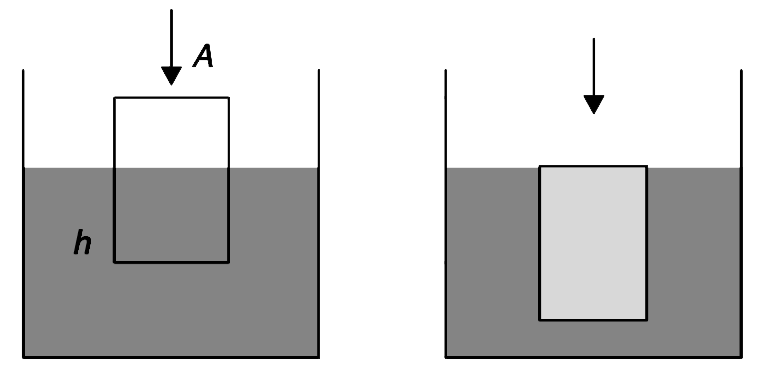
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylindrical wooden block of density half the density of water is flo...
Text Solution
|
- A wooden block is floating in a water tank. The block is pressed to it...
Text Solution
|
- A woman of mass 50 kg stands on a wooden block placed over a tank of w...
Text Solution
|
- A cylindrical wooden float whose base area S and the height H drift on...
Text Solution
|
- A wooden block of cross sectional area A (in shape of a rectangle) has...
Text Solution
|
- A cylindrical wooden block of density half the density of water is flo...
Text Solution
|
- A cylindrical object of the area of cross section 5 cm^(2) floats (lat...
Text Solution
|
- two cubical blocks identical in dimensions float in water in such a wa...
Text Solution
|
- 120 kg ভরের একটি কাঠের ব্লক জলে ভাসে। কাঠের ব্লকের ঘনত্ব 600 kg/m | ক...
Text Solution
|