Home
Class 11
PHYSICS
The graph betwee sqrt(E) and (1)/(p) is ...

The graph betwee `sqrt(E)` and `(1)/(p)` is (E=kinetic energy and p= momentum)

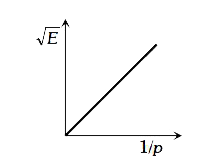
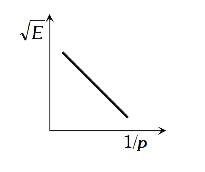
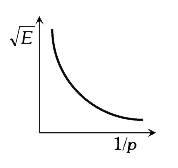
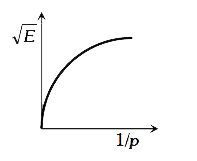
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
`KE=p^2/(2m) implies sqrtE =p/(sqrt2m)implies sqrtE/p ` = constant
Graph between p and `sqrtE` is parabola but graph between `1/4` and `sqrtE` is hyperbola.
Promotional Banner

Similar Questions

Explore conceptually related problems

The graph between linear monentum (p) and Kinetic energy (k) is best represented by

The relation between kinetic energy K and linear momentum p of a particle is represented by

The momentum of a body is p and its kinetic energy is E. Its momentum becomes 2p. Its kinetic energy will be

(a) A proton is moving at a speed much less than the speed of light. It has kinetic energy K_1 and momentum p_1 . If the momentum of the proton is doubled, so p_2 = 2 p_1 , how is its new kinetic energy K_2 related to K-1 ? (b)A photon with energy E_1 has momentum p_1 . if another photon has momentum p_2 that is twice p_1 , how is the energy E_2 of the second photon related to E_1 ?

An electron with speed v and a photon with speed c have the same de-Broglic wavelength. If the kinetic energy and momentum of electron is E_(e) and P_(e) and that of photon is E_(ph) and P_(ph) respectively, then correct statement is -

The curve between log_(e) L and log_(e) P is (L is the angular momentum and P is the linear momentum).

Which of the following graphs represents the graphical relation between momentum (p) and kinetic energy (K) for a body in motion?

Which one of the following correctly represents the variation between linear momentum (P) and kinetic energy (E) ofa body?

Relation between kinetic energy and momentum Let us consider a body of mass 'm' having a velocity 'v', then momentum of the body P = mass xx velocity P = m xx v rArr v = (P)/(m) " "...(1) From definition, kinetic energy (K.E) of the body K.E = (1)/(2) mv^(2)" "...(2) Now putting the value of (1) in (2) we have K.E = (1)/(2)m ((P)/(m))^(2) K.E. = (1)/(2)m (P^(2))/(m^(2)) = (1)/(2) (P^(2))/(m) = (P^(2))/(2m)" "...(3) Thus we can write P^(2) = 2m xx K.E rArr P = sqrt(2m xx K.E) Thus momentum = sqrt(2 xx "mass" xx "kinetic energy") What will be the momentum of a body of mass 100 g having kinetic energy of 20 J ?