Home
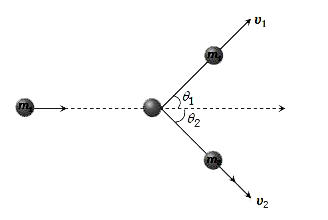
Class 11
PHYSICS
A sphere of mass m moving with a uniform...

A sphere of mass m moving with a uniform velocity v hits another identical sphere at rest. If the coefficient of restitution is e, the ratio of the velocities of the two sphere after the collision is `(e-1)/(e+1)`.

A

0

B

`45^@`

C

`90^@`

D

`180^@`

Text Solution

Verified by Experts

The correct Answer is:
C
For perfectly elastic collision
`theta_1 +theta_2 = 90^@`
`implies theta =90^@`
Promotional Banner

Similar Questions

Explore conceptually related problems

A particle of mass m moving with a constant velocity v hits another identical stationary particle. If coefficient of restitution is e then ratio of velocities of two particles after collision is

A particle of mass m moving with a constant velocity v hits another identical stationary particle. If coefficient of restitution is e then ratio of velocities of two particles after collision is

A sphere A impinges directly on an identical sphere B at rest. If coefficient of restitution is e , the ratio of velocities of A and B after collision is

Sphere A of mass 'm' moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres v_(A):v_(B) after collision will be :

A ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?

A sphere of mass m moving with a constant velocity hits another stationary sphere of the same mass, if e is the coefficient of restitution, then ratio of speed of the first sphere to the speed of the second sphere after collision will be

A sphere of mass m moving with constant velocity u , collides with another stationary sphere of same mass. If e is the coefficient of restitution, the ratio of the final velocities of the first and second sphere is