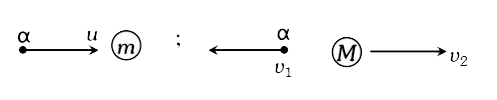A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An alpha-particle of mass m suffers 1-dimentinal eleastic collision wi...
Text Solution
|
- And alpha-particle with kinetic enregy T(alpha) = 7.0 MEV is scattered...
Text Solution
|
- A radioactive nucleus of mass number A, initially at rest, emits an al...
Text Solution
|
- A stationary radioactive nucleus of mass 210 units disintegrates into ...
Text Solution
|
- An alpha-particle of mass m suffers 1-dimentinal eleastic collision wi...
Text Solution
|
- An alpha-particle of mass m suffers 1 -dimentinal eleastic collision w...
Text Solution
|
- A radioactive nucleus of mass number A, initially at rest, emits an al...
Text Solution
|
- An alpha-particlee of mass m suffers one dimensional elastic collision...
Text Solution
|
- In Rutherford experiment alpha – particles are scattered by nucleus ha...
Text Solution
|