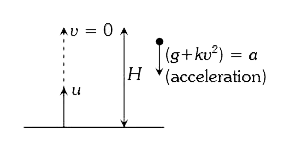A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small ball of mass m is thrown upward with velocity u from the groun...
Text Solution
|
- (a) A ball is thrown vertically upward with speed 10 m//s and it retur...
Text Solution
|
- A ball is thrown vertically upwards from the top of tower of height h ...
Text Solution
|
- A ball is thrown upwards with a speed u from a height h above the grou...
Text Solution
|
- A ball is thrown vertically upward with a velocity of 20 m/s. Calculat...
Text Solution
|
- A ball is thrown vertically upwards with a velocity u from the ground....
Text Solution
|
- A ball is thrown with velocity V0 from ground in vertical upward direc...
Text Solution
|
- A small ball of mass m is thrown upward with velocity u from the groun...
Text Solution
|
- A ball is thrown vertically upwards from the ground at a height of h a...
Text Solution
|