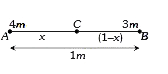A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two point masses A and B having masses in the ratio 4:3 are separated ...
Text Solution
|
- Gravitational force between two point masses m and M separated by a di...
Text Solution
|
- Two point masses A and B having masses in the ratio 4:3 are separated ...
Text Solution
|
- Two bodies A and B having masses 20kg and 40kg are separated by 10 m. ...
Text Solution
|
- Gravitational force between a point mass m and M separated by a distan...
Text Solution
|
- The electrostatic force between two point charges and the gravitationa...
Text Solution
|
- दो वस्तुओ A तथा B के बीच गुरुत्वाकर्षण बल ज्ञात करें यदि एक वस्तु A का...
Text Solution
|
- A एवं B द्रव्यमान बिंदुओं के द्रव्यमान 4 : 3 के अनुपात में हैं, जिन्हे...
Text Solution
|
- Gravitational force between two point masses m and M seperated by a di...
Text Solution
|