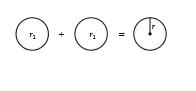
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two spherical soap bubbles of radii r1 and r2 in vacuume collapse unde...
Text Solution
|
- Two spherical soap bubbles of radii r1 and r2 in vacuume collapse unde...
Text Solution
|
- A soap bubble in vacuum has a radius of 3 cm ad another soap bubble in...
Text Solution
|
- Two spherical soap bubbles of radii a and b in vacuum coalesce under i...
Text Solution
|
- Two spherical soap bubbles of a radii 1 cm and 2 cm vacuum coalesce un...
Text Solution
|
- Two spherical soap bubbles of radii r(1) and r(2) in vacuum combine un...
Text Solution
|
- Two spherical soap bubbles of radii a and b in vacuum coalesce under i...
Text Solution
|
- Two spherical soap bubbles of radii a and b in vacuum coalesce under i...
Text Solution
|
- Two spherical soap bubbles of radii a and b in vacuum coalesce under i...
Text Solution
|