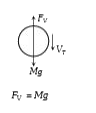
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A rain drop with radus 1.5 mm falls from a cloud at a height 1200 m fr...
Text Solution
|
- A drop of water of radius 0.0015 mm is falling in air. If the coeffici...
Text Solution
|
- A drop of water of radius 0.001 mm is falling in air. If the coeffcien...
Text Solution
|
- A drop of water of radius 0.0015 mm is falling in air .If the coeffici...
Text Solution
|
- लगभग गोलाकार 0.01 mm त्रिज्या वाली वर्षा कि बूंदे हवा में ऊर्ध्वाधर द...
Text Solution
|
- A drop of radius 2xx10^(-5) and density 1.2xx10^(3)kg//m^(3) falls thr...
Text Solution
|
- If an oil drop of density 0.95xx10^(3)kg//m^(3) and radius 10^(-4) cm ...
Text Solution
|
- A rain drop with radus 1.5 mm falls from a cloud at a height 1200 m fr...
Text Solution
|
- A rain drop with radus 1.5 mm falls from a cloud at a height 1200 m fr...
Text Solution
|