A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
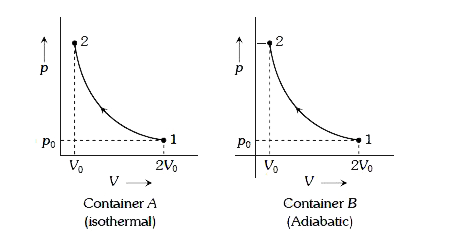
- Consider two containers A and B containing identical gases at the same...
Text Solution
|
- Consider two containers A and B containing identical gases at the same...
Text Solution
|
- A gas is compressed isothermally to half its initial volume. The same ...
Text Solution
|
- Consider two containers A and B containing identical gases at the same...
Text Solution
|
- Consider two containers A and B containing identical gases at the same...
Text Solution
|
- Consider two containers A and B containing identical gases at the same...
Text Solution
|
- A gas is compressed isothermally to half its initial volume. The same ...
Text Solution
|
- Consider two containers A and B containing identical gases at the same...
Text Solution
|
- Consider two containers A and B containing identical gases at the same...
Text Solution
|