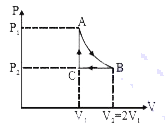
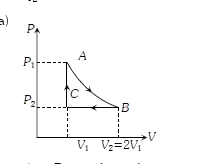
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- n mole a perfect gas undergoes a cyclic process ABCA (see figure) cons...
Text Solution
|
- An ideal gas is initially at P1,V1 is expands to P2,V2 and then compre...
Text Solution
|
- The change in the entropy of a 1 mole of an ideal gas which went throu...
Text Solution
|
- An ideal monatomic gas undergoes a cyclic process ABCA as shown in the...
Text Solution
|
- समतापी प्रक्रम में 1 मोल आदर्श गैस की अवस्था (P1,V1 ) से (P2,V2 ,) तक ...
Text Solution
|
- What is an isothermal process? State essential conditions for such a p...
Text Solution
|
- A certain mass of an ideal gas at pressure P1 is adiabatically expande...
Text Solution
|
- Initially a gas of diatomic molecules is contained in a cylinder of vo...
Text Solution
|
- Two samples A and B of a gas are initially at the same temperature and...
Text Solution
|