Home
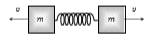
Class 11
PHYSICS
Two blocks each of mass m are connected ...

Two blocks each of mass m are connected to a spring of spring constant k. if both are given velocity v in opposite directions, then the maximum elongation of the spring is

A

`sqrt((mv^(2))/(k))`

B

`sqrt((2mv^(2))/(k))`

C

`sqrt((mv^(2))/(2k))`

D

`2sqrt((mv^(2))/(k))`

Text Solution

Verified by Experts

The correct Answer is:
B
Law of conservation of energy-
`(1)/(2) mv^(2)+(1)/(2)mv^(2)=(1)/(2)kx^(2)`
`implies mv^(2)=(1)/(2) kx^(2) implies x=sqrt((2mv^(2))/(k))`.
Promotional Banner

Similar Questions

Explore conceptually related problems

A block of mass m suspended from a spring of spring constant k . Find the amplitude of S.H.M.

2 mass of block 2 kg & 4 kg are attached to a stiffness spring 100 N/m. 2 kg mass is given velocity 2 m/s & 4 kg to 4 m/s in same direction. Find maximum elongation in the spring during the motion of two blocks.

Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be

Two blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then The kinetic energy of the A-B system at maximum compression of the spring is mv^(2)//4 The maximum compression of the spring vsqrt(m//3k) The kinetic energy of the A-B system at maximum compression The maximum coppression of the spring is vsqrt(m//k)

Blocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.

Two blocks of masses m_1 and m_2 are connected by a spring of spring constant k figure. The block of mass m_2 is given a shapr imulse so that it acquires a velocity v_0 twoards right. Find a. the velocity of the cenre of mas b. the maximum elongation that teh spring will suffer.

A block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is

A disc of mass m is connected with an ideal spring of stiffness k . If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is: