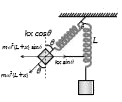
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small mass m attached to one end of a spring with a negligible mass ...
Text Solution
|
- A thin uniform vertical rod of mass m and length l pivoted at point O ...
Text Solution
|
- In a spring- mass system , the length of the spring is L, and it has a...
Text Solution
|
- A particle of mass m is fixed to one end of a light spring of force co...
Text Solution
|
- A mass m attached to spring of natural length l0 and spring constant k...
Text Solution
|
- किसी घर्षण रहित क्षैतिज मेज पर 1 मीटर लम्बाई की स्प्रिंग (k = 100 न्य...
Text Solution
|
- A small mass m attached to one end of a spring with a negligible mass ...
Text Solution
|
- तनयहीन लम्बाई L तथा नगण्य द्रव्यमान की एक स्प्रिंग जिसके एक सिरे से क...
Text Solution
|
- A mass m attached to spring of natural length l0 and spring constant k...
Text Solution
|