Home
Class 11
PHYSICS
Two masses m(1)=1.0 kg and m(2)=0.5 ...

Two masses `m_(1)=1.0 kg and m_(2)=0.5 kg ` are suspended together by a massless spring of force constant, `k=12.5 Nm^(-1)`. When they are in equillibrium position, `m_(1)` is gently removed. Calculate the angular frequency and the amplitude of oscillation of `m_(2)`. Given `g=10 ms^(-2)`.

Text Solution

Verified by Experts

The correct Answer is:
`0.8`
Let y be the extension in the length of the spring when both ` m_(1) and m_(2)` are suspended
Then, ` F = (m_(1) + m_(2)) g = Ky`
or ` y = ((m_(1) + m_(2))g)/(K)`
Let the extension be reduced to y. when `m_(1)` is removed then
`m_(2) g = Ky.`
or ` y. = (m_(2) g)/( K)`
`:. y - y. = ((m_(1) + m_(2))g)/(K) - (m_(2) g)/( K)`
This will be the amplitude of oscillation of `m_(2)`
`:.` Amplitude, ` A = (m_(1) g)/( K) = (1.0 xx 10)/( 12.5) = 0.8 m`
Angular frequency
`omega = sqrt((K)/( m_(2))) = sqrt(( 12.5)/(0.5)) = 5 rad s^(-1)`
Promotional Banner

Similar Questions

Explore conceptually related problems

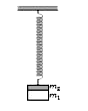
Two masses m_(1) = 1kg and m_(2) = 0.5 kg are suspended together by a massless spring of spring constant 12.5 Nm^(-1) . When masses are in equilibrium m_(1) is removed without disturbing the system. New amplitude of oscillation will be

Two mass m_(1) and m_(2) are suspended from a massless spring of force constant k. When the masses are in equilibrium, m_(1) is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.

Two masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000 Nm^(-1) . When the masses are in equilibrium 8 kg is removed without disturbing the system . The amplitude of oscillation is

Two masses m_(1) and m_(2) are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m_(1) is gently removed. The angular frequency and amplitude of oscillation of m_(2) will be respectively

Two masses m_(1) and m_(2) are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m_(1) is removed. Frequency and amplitude of oscillation of m_(2) are

Two masses m_(1) and m_(2) are suspended together by a massless spring of constant K. When the masses are in equilibrium, m_(1) is removed without disturbing the system. Then the angular frequency of oscillation of m_(2) is -

Two masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

Two masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.

Two masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is

Two bodies with masses m_(1) = 1kg and m_(2) = 2kg are connected by a spring of force constant k=24Nm^(-1) . The left ball is imparted an initial velocity v_(0) =12 cm/s. Find (a) the frequency of the oscillations (b) the energy and the amplitude of the osciallations.