A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
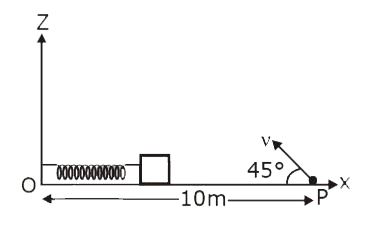
- A small block is connected to one end of a massless spring of un-stret...
Text Solution
|
- A block of mass 2.0 kg is moving on a frictionless horizontal surface ...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- एक द्रव्यमानहीन स्प्रिंग की तनावहीन लम्बाई 4.9 सेमी है | इसका एक सिरा ...
Text Solution
|
- A small block is connected to one end of a massless spring of un-stret...
Text Solution
|