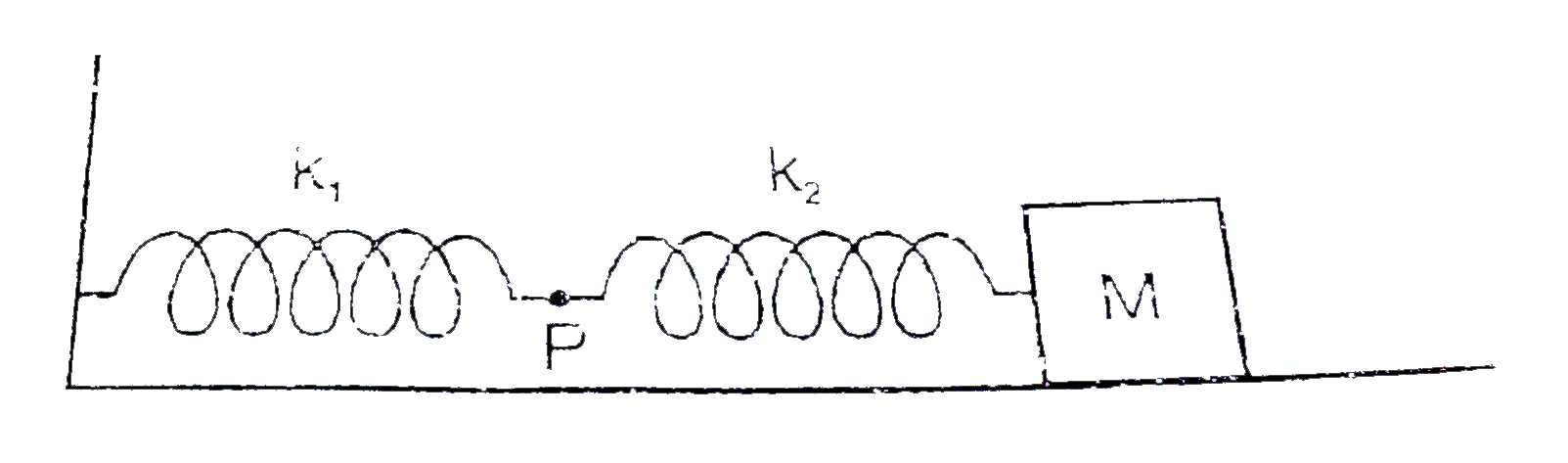A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The mass M shown in the figure oscillates in simple harmnonic motion a...
Text Solution
|
- What will happen to the motion of simple pendulum if the amplitude of ...
Text Solution
|
- The mass M shown in the figure oscillates in simple harmonic motion wi...
Text Solution
|
- The mass M shown in the figure oscillates in simple harmnonic motion a...
Text Solution
|
- The acceleration of a certain simple harmonic oscillator is given by ...
Text Solution
|
- क्या कम आयाम की दोलन गति सदैव सरल आवर्त गति होती है ?
Text Solution
|
- A simple harmonic motion of amplitude A has a time period T. The accel...
Text Solution
|
- The motion of a simple pendulum when it oscillates with small amplitud...
Text Solution
|
- सरल आवर्त गति में दोलनका आवर्तकाल 0.5 सेकण्ड तथा आयाम 0.1 मी. है। दोलक...
Text Solution
|