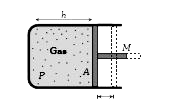
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylinder piston of mass M sides smoothly inside a long cylinder clos...
Text Solution
|
- An ideal gas enclosed in a cylindrical container supports a freely mov...
Text Solution
|
- A cylinder piston of mass M sides smoothly inside a long cylinder clos...
Text Solution
|
- A vertical closed cylinder is separated into two parts by a frictionle...
Text Solution
|
- A vertical closed cylinder is separated into two parts by a frictionle...
Text Solution
|
- A ideal gas is kept in a cylinder of cross sectional area A and volume...
Text Solution
|
- A piston of mass m can move without friction in a uniform closed cylin...
Text Solution
|
- A block of mass ‘m’ rests on a piston executing S.H.M. of period 1sec....
Text Solution
|
- A cylindrical piston of mass M slides smoothly inside a long cylinder ...
Text Solution
|