A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
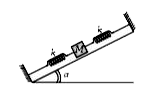
- On a smooth inclined plane, a body of mass M is attached between two ...
Text Solution
|
- On a smooth inclined plane a body of mass M is attached between two sp...
Text Solution
|
- On a smooth inclined plane, a body of mass M is attached between two s...
Text Solution
|
- On a smooth inclined plane a body of mass M is attached between two sp...
Text Solution
|
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- If k is the force constant of the spring and mu is the coefficient of ...
Text Solution
|
- A mass m is attached to the free end of a massless spring of spring co...
Text Solution
|
- m द्रव्यमान का एक पिण्ड एक स्प्रिंग से बँधा हुआ है और दोलन करता है। यद...
Text Solution
|
- A spring of spring constant 'k' is supported from one end and tied by ...
Text Solution
|